| 5. LA INTEGRAL Y TÉCNICAS DE INTEGRACIÓN | 5.13 Integración numérica |
Ejercicios propuestos para el capítulo 5.13
Calcule las siguientes integrales usando la regla del punto medio, la regla trapezoidal o la regla de Simpson como se indica. (Redondea las respuestas a tres lugares decimales):

regla trapezoidal; n = 5
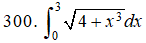
regla trapezoidal; n = 6

regla trapezoidal; n = 3

regla del punto medio; n = 6

regla del punto medio; n = 3

regla del punto medio; n = 8

regla trapezoidal; n = 4
306. Halla el valor exacto de Encuentre el error de aproximación entre el valor exacto y el valor calculado usando la regla trapezoidal con cuatro subdivisiones. Dibuja una gráfica para ilustrar.
Encuentre el error de aproximación entre el valor exacto y el valor calculado usando la regla trapezoidal con cuatro subdivisiones. Dibuja una gráfica para ilustrar.
Aproxime la integral a tres lugares decimales usando la regla indicada.
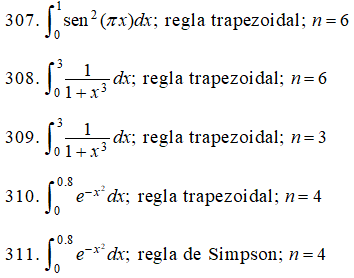

316. Evalúe exactamente y demuestre que el resultado es π/4. Luego, encuentra el valor aproximado de la integral usando la regla trapezoidal con n = 4 subdivisiones. Utilice el resultado para aproximar el valor de π.
exactamente y demuestre que el resultado es π/4. Luego, encuentra el valor aproximado de la integral usando la regla trapezoidal con n = 4 subdivisiones. Utilice el resultado para aproximar el valor de π.
317. Estime usando la regla del punto medio con cuatro subdivisiones y con una aproximación de cuatro decimales.
usando la regla del punto medio con cuatro subdivisiones y con una aproximación de cuatro decimales.
318. Estime usando la regla del trapecio con ocho subdivisiones y con una aproximación de cuatro cifras decimales.
usando la regla del trapecio con ocho subdivisiones y con una aproximación de cuatro cifras decimales.
319. Use la regla trapezoidal con cuatro subdivisiones para estimar con cuatro lugares decimales.
con cuatro lugares decimales.
320. Use la regla trapezoidal con cuatro subdivisiones para estimar Compare este valor con el valor exacto y encuentre la estimación del error.
Compare este valor con el valor exacto y encuentre la estimación del error.
321. Usando la regla de Simpson con cuatro subdivisiones, encuentre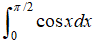
322. Muestre que el valor exacto de Encuentre el error absoluto si aproxima la integral usando la regla del punto medio con 16 subdivisiones.
Encuentre el error absoluto si aproxima la integral usando la regla del punto medio con 16 subdivisiones.
323. Dado , use la regla trapezoidal con 16 subdivisiones para aproximar la integral y encontrar el error absoluto.
, use la regla trapezoidal con 16 subdivisiones para aproximar la integral y encontrar el error absoluto.
324. Encuentre un límite superior para el error al estimar usando la regla trapezoidal con seis pasos.
usando la regla trapezoidal con seis pasos.
325. Encuentre un límite superior para el error al estimar usando la regla trapezoidal con siete subdivisiones.
usando la regla trapezoidal con siete subdivisiones.
326. Encuentre un límite superior para el error al estimar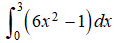 usando la regla de Simpson con n = 10 pasos.
usando la regla de Simpson con n = 10 pasos.
327. Encuentre un límite superior para el error al estimar usando la regla de Simpson con n = 10 pasos.
usando la regla de Simpson con n = 10 pasos.
328. Encuentre un límite superior para el error al estimar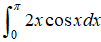 usando la regla de Simpson con cuatro pasos.
usando la regla de Simpson con cuatro pasos.
329. Estime el número mínimo de subintervalos necesarios para aproximar la integral con una magnitud de error menor que 0,0001 usando la regla trapezoidal.
con una magnitud de error menor que 0,0001 usando la regla trapezoidal.
330. Determine un valor de n tal que la regla trapezoidal se aproxime a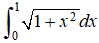 con un error de no más de 0.01.
con un error de no más de 0.01.
331. Estime el número mínimo de subintervalos necesarios para aproximar la integral con un error de magnitud menor que 0,0001 usando la regla trapezoidal.
con un error de magnitud menor que 0,0001 usando la regla trapezoidal.
332. Estime el número mínimo de subintervalos necesarios para aproximar la integral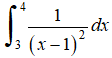 con una magnitud de error de menos de 0,0001 usando la regla trapezoidal.
con una magnitud de error de menos de 0,0001 usando la regla trapezoidal.
333. Use la regla de Simpson con cuatro subdivisiones para aproximar el área bajo la función de densidad de probabilidad desde x = 0 hasta x = 0.4.
desde x = 0 hasta x = 0.4.
334. Use la regla de Simpson con n = 14 para aproximar (con tres decimales) el área de la región delimitada por las gráficas de y = 0, x = 0 y x = π/2.
335. La longitud de un arco de la curva y = 3sen(2x) está dada por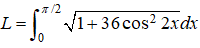 Estime L usando la regla trapezoidal con n = 6.
Estime L usando la regla trapezoidal con n = 6.
336. La longitud de la elipse x = acost, y = bsent, 0 ≤ t ≤ 2π está dada por donde e es la excentricidad de la elipse. Utilice la regla de Simpson con n = 6 subdivisiones para estimar la longitud de la elipse cuando a = 2 y e = 1/3.
donde e es la excentricidad de la elipse. Utilice la regla de Simpson con n = 6 subdivisiones para estimar la longitud de la elipse cuando a = 2 y e = 1/3.
337. Estime el área de la superficie generada al girar la curva y = cos2x, 0 ≤ x ≤ π/4 sobre el eje x. Utilice la regla trapezoidal con seis subdivisiones.
338. Estime el área de la superficie generada al girar la curva y = 2x², 0 ≤ x ≤ 3 alrededor del eje x. Utilice la regla de Simpson con n = 6.
339. La tasa de crecimiento de cierto árbol (en pies) está dada por donde t es el tiempo en años. Estime el crecimiento del árbol hasta el final del segundo año usando la regla de Simpson, usando dos subintervalos. (Redondea la respuesta a la centésima más cercana).
donde t es el tiempo en años. Estime el crecimiento del árbol hasta el final del segundo año usando la regla de Simpson, usando dos subintervalos. (Redondea la respuesta a la centésima más cercana).
340. [T] Usa una calculadora para aproximar usando la regla del punto medio con 25 subdivisiones. Calcule el error relativo de aproximación.
usando la regla del punto medio con 25 subdivisiones. Calcule el error relativo de aproximación.
341. [T] Dado aproxima el valor de esta integral usando la regla trapezoidal con 16 subdivisiones y determina el error absoluto.
aproxima el valor de esta integral usando la regla trapezoidal con 16 subdivisiones y determina el error absoluto.
342. Dado que conocemos el Teorema fundamental del cálculo, ¿por qué querríamos desarrollar métodos numéricos para integrales definidas?
343. La tabla representa las coordenadas (x, y) que dan el límite de un lote. Las unidades de medida son metros. Use la regla trapezoidal para estimar la cantidad de metros cuadrados de terreno que hay en este lote.
| x | y | x | y |
|---|---|---|---|
| 0 | 125 | 600 | 95 |
| 100 | 125 | 700 | 88 |
| 200 | 120 | 800 | 75 |
| 300 | 112 | 900 | 35 |
| 400 | 90 | 1000 | 0 |
| 500 | 90 |
344. Elija la respuesta correcta. Cuando se usa la regla de Simpson para aproximar la integral definida, es necesario que el número de particiones sea____
- un número par
- número impar
- ya sea un número par o impar
- un múltiplo de 4
345. La suma de “Simpson” se basa en el área debajo de ____.
346. La fórmula de error de la regla de Simpson depende de___.
- f (x)
- f ′(x)
- f ⁽⁴⁾(x)
- el número de pasos.
