| 3.8 Diferenciación implícita |
Ejercicios propuestos para el Capítulo 3.8
Para los siguientes ejercicios, usa la diferenciación implícita para encontrar \(\frac{dy}{dx}\):
300. \(x^2 – y^2 = 4\)
301. \(6x^2 + 3y^2 = 12\)
302. \(x^2y = y – 7\)
303. \(3x^3 + 9xy^2 = 5x^3\)
304. \(xy – \cos(xy) = 1\)
305. \(y\sqrt{x + 4} = xy + 8\)
306. \(-xy – 2 = \frac{x}{7}\)
307. \(y\sin(xy) = y^2 + 2\)
308. \((xy)^2 + 3x = y^2\)
309. \(x^3y + xy^3 = -8\)
Para los siguientes ejercicios, encuentra la ecuación de la recta tangente a la gráfica de la ecuación dada en el punto indicado. Usa una calculadora o software de computadora para graficar la función y la recta tangente:
310. [T] \(x^4y – xy^3 = -2, (-1, -1)\)
311. [T] \(x^2y^2 + 5xy = 14, (2, 1)\)
312. [T] \(\tan(xy) = y, \left(\frac{\pi}{4}, 1\right)\)
313. [T] \(xy^2 + \sin(\pi y) – 2x^2 = 10, (2, -3)\)
314. [T] \(\frac{x}{y} + 5x – 7 = -\frac{3}{4}y, (1, 2)\)
315. [T] \(xy + \sin(x) = 1, \left(\frac{\pi}{2}, 0\right)\)
316. [T] La gráfica de un folio de Descartes con ecuación \(2x^3 + 2y^3 – 9xy = 0\) se da en la siguiente gráfica.
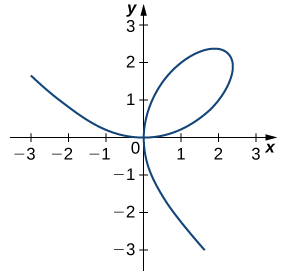
a. Encuentra la ecuación de la recta tangente en el punto \((2, 1)\). Grafica la recta tangente junto con el folio.
b. Encuentra la ecuación de la recta normal a la recta tangente en a. en el punto \((2, 1)\).
317. Para la ecuación \(x^2 + 2xy – 3y^2 = 0\),
a. Encuentra la ecuación de la recta normal a la recta tangente en el punto \((1, 1)\).
b. ¿En qué otro punto la recta normal en a. interseca la gráfica de la ecuación?
318. Encuentra todos los puntos en la gráfica de \(y^3 – 27y = x^2 – 90\) en los que la recta tangente es vertical.
319. Para la ecuación \(x^2 + xy + y^2 = 7\),
a. Encuentra la(s) intersección(es) con el eje x.
b. Encuentra la(s) pendiente(s) de la(s) recta(s) tangente(s) en la(s) intersección(es) con el eje x.
c. ¿Qué indica(n) el(los) valor(es) en b. sobre la(s) recta(s) tangente(s)?
320. Encuentra la ecuación de la recta tangente a la gráfica de la ecuación \(\sin^{-1}x + \sin^{-1}y = \frac{\pi}{6}\) en el punto \(\left(0, \frac{1}{2}\right)\).
321. Encuentra la ecuación de la recta tangente a la gráfica de la ecuación \(\tan^{-1}(x + y) = x^2 + \frac{\pi}{4}\) en el punto \((0, 1)\).
322. Encuentra \(y’\) e \(y”\) para \(x^2 + 6xy – 2y^2 = 3\).
323. [T] El número de teléfonos celulares producidos cuando se gastan \(x\) dólares en mano de obra y \(y\) dólares se gastan en capital invertido por un fabricante se puede modelar mediante la ecuación \(60x^{3/4}y^{1/4} = 3240\).
a. Encuentra \(\frac{dy}{dx}\) y evalúa en el punto \((81, 16)\).
b. Interpreta el resultado de a.
324. [T] El número de automóviles producidos cuando se gastan \(x\) dólares en mano de obra y \(y\) dólares se gastan en capital invertido por un fabricante se puede modelar mediante la ecuación \(30x^{1/3}y^{2/3} = 360\).
(Tanto \(x\) como \(y\) se miden en miles de dólares).
a. Encuentra \(\frac{dy}{dx}\) y evalúa en el punto \((27, 8)\).
b. Interpreta el resultado de a.
325. El volumen de un cono circular recto de radio \(x\) y altura \(y\) está dado por \(V = \frac{1}{3}\pi x^2 y\). Supón que el volumen del cono es constante. Encuentra \(\frac{dy}{dx}\) cuando \(x = 4\) e \(y = 16\).
Para los siguientes ejercicios, considera una caja rectangular cerrada con una base cuadrada de lado \(x\) y altura \(y\):
326. Encuentra una ecuación para el área superficial de la caja rectangular, \(S(x, y)\).
327. Si el área superficial de la caja rectangular es de 78 pies cuadrados, encuentra \(\frac{dy}{dx}\) cuando \(x = 3\) pies e \(y = 5\) pies.
Para los siguientes ejercicios, usa la diferenciación implícita para determinar \(y’\). ¿Concuerda la respuesta con las fórmulas que hemos determinado previamente?:
328. \(x = \sin y\)
329. \(x = \cos y\)
330. \(x = \tan y\)
