| 9. Ecuaciones diferenciales | 9.7. Soluciones en serie de ecuaciones lineales de segundo orden | Ejercicios propuestos para el Capítulo 9.7.6 |
9.7.6 El método de Frobenius II
En esta sección discutimos un método para encontrar dos soluciones de Frobenius linealmente independientes de una ecuación lineal homogénea de segundo orden cerca de un punto singular regular en el caso donde la ecuación indicial tiene una raíz real repetida. Como en la sección anterior, consideramos ecuaciones que se pueden escribir como
x2(α0 + α1x + α2x2)y′′ + x(β0 + β1x + β2x2)y′ + (γ0 + γ1x + γ2x2)y = 0 (9.7.6.1)
donde α0 ≠ 0. Suponemos que la ecuación indicial p0(r) = 0 tiene una raíz real repetida r1. En este caso, el Teorema 9.7.5.3 implica que (9.7.6.1) tiene una solución de la forma
pero no proporciona una segunda solución y2 tal que {y1, y2} sea un conjunto fundamental de soluciones. La siguiente extensión del Teorema 9.7.5.2 proporciona una forma de encontrar una segunda solución.
Teorema 9.7.6.1
Sea
(9.7.6.2)
donde α0 ≠ 0 y definimos
Suponga que r es un número real tal que p0(n + r) es distinto de cero para todos los enteros positivos n, y defina
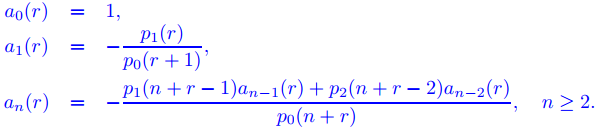
Entonces la serie de Frobenius
(9.7.6.3)
satisface
(9.7.6.4)
Además,
(9.7.6.5)
y
(9.7.6.6) ♦
Prueba:
El Teorema 9.7.5.2 implica (9.7.6.4). Derivando formalmente con respecto a r en (9.7.6.3) se obtiene
lo que prueba (9.7.6.5).
Para probar que ∂y(x, r)/∂r satisface (9.7.6.6), vemos y en (9.7.6.2) como una función y = y(x, r) de dos variables, donde la prima indica diferenciación parcial con respecto a x; de este modo,
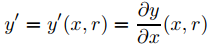y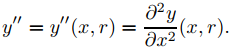 
Con esta notación podemos usar (9.7.6.2) para reescribir (9.7.6.4) como
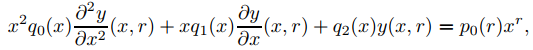(9.7.6.7)
donde
Derivando ambos lados de (9.7.6.7) con respecto a r se obtiene
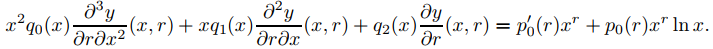
Al cambiar el orden de diferenciación en los dos primeros términos de la izquierda, podemos reescribir esto como
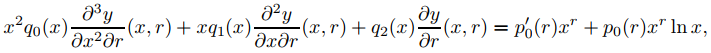
o
que es equivalente a (9.7.6.6). ♦
Teorema 9.7.6.2
Sea L como en el Teorema 9.7.6.1 y suponga que la ecuación indicial p0(r) = 0 tiene una raíz real repetida r1. Entonces
y
(9.7.6.8)
forman un conjunto fundamental de soluciones de Ly = 0. ♦
Prueba:
Dado que r1 es una raíz repetida de p0(r) = 0, el polinomio indicial se puede factorizar como
p0(r) = α0(r − r1)2,
por lo que
p0(n + r1) = α0n2,
que es distinto de cero si n > 0. Por lo tanto, los supuestos del Teorema 9.7.6.1 se cumplen con r = r1, y (9.7.6.4) implica que Ly1 = p0(r1)xr1 = 0. Dado que
p′0(r) = 2α(r − r1)
se sigue que p′0(r1) = 0, entonces (9.7.6.6) implica que
Esto prueba que y1 e y2 son ambas soluciones de Ly = 0. Dejamos como ejercicio la prueba de que {y1, y2} es un conjunto fundamental (Ejercicio 53). ♦
Ejemplo ilustrativo 9.7.6.1
Encuentre un conjunto fundamental de soluciones de
x2(1 − 2x + x2)y′′ − x(3 + x)y′ + (4 + x)y = 0. (9.7.6.9)
Calcule solo los términos relacionados con xn + r1, donde 0 ≤ n ≤ 4 y r1 es la raíz de la ecuación indicial.
Solución:
Para la ecuación dada, los polinomios definidos en el Teorema 9.7.6.1 son
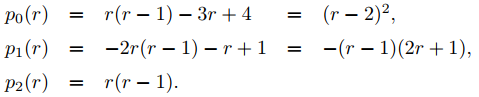
Como r1 = 2 es una raíz repetida del polinomio indicial p0, el Teorema 9.7.6.2 implica que
y 
(9.7.6.10)
forman un conjunto fundamental de soluciones de Frobenius de (9.7.6.9). Para encontrar los coeficientes en estas series, usamos las fórmulas de recurrencia del Teorema 9.7.6.1:
(9.7.6.11)
Diferenciando, obtenemos
(9.7.6.12)
Establecer r = 2 en (9.7.6.11) y (9.7.6.12) produce
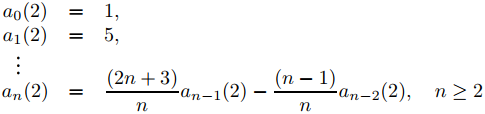(9.7.6.13)
y
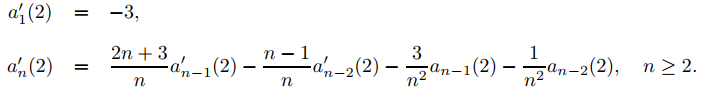(9.7.6.14)
Calcular recursivamente con (9.7.6.13) y (9.7.6.14) produce
y
Sustituyendo estos coeficientes en (9.7.6.10) se obtiene
y
♦
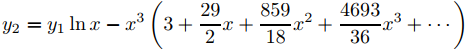Dado que la fórmula de recurrencia (9.7.6.11) involucra tres términos, no es posible obtener una fórmula explícita simple para los coeficientes en las soluciones de Frobenius de (9.7.6.9). Sin embargo, como vimos en las secciones anteriores, la fórmula de recurrencia para {an(r)} involucra solo dos términos si α1 = β1 = γ1 = 0 o α2 = β2 = γ2 = 0 en (9.7.6.1). En este caso, a menudo es posible encontrar fórmulas explícitas para los coeficientes. Los siguientes dos ejemplos ilustran esto.
Encuentre un conjunto fundamental de soluciones de Frobenius de
2x2(2 + x)y′′ + 5x2y′ + (1 + x)y = 0. (9.7.6.15)
Dé fórmulas explícitas para los coeficientes en las soluciones.
Solución:
Para la ecuación dada, los polinomios definidos en el Teorema 9.7.6.1 son
Como r1 = 1/2 es un cero repetido del polinomio indicial p0, el Teorema 9.7.6.2 implica que
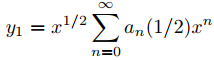(9.7.6.16)
y
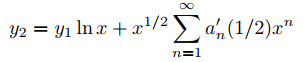(9.7.6.17)
forman un conjunto fundamental de soluciones de Frobenius de (9.7.6.15). Como p2 ≡ 0, las fórmulas de recurrencia del Teorema 9.7.6.1 se reducen a
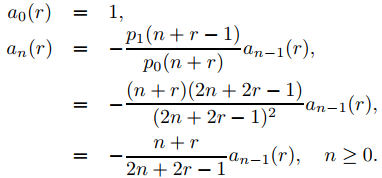
Le dejamos a usted para mostrar que
(9.7.6.18)
Establecer r = 1/2 produce
(9.7.6.19)
Sustituyendo esto en (9.7.6.16) se obtiene
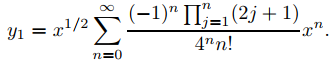
Para obtener y2 en (9.7.6.17), debemos calcular a′n(1/2) para n = 1, 2,. . . . Haremos esto por diferenciación logarítmica. De (9.7.6.18),
Por lo tanto
Derivando con respecto a r, obtenemos
Por lo tanto
Poniendo r = 1/2 aquí y recordando (9.7.6.19) se obtiene
(9.7.6.20)
Dado que
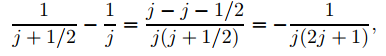
(9.7.6.20) se puede reescribir como
Por lo tanto, de (9.7.6.17),
♦
.
Ejemplo ilustrativo 9.7.6.3
Encuentre un conjunto fundamental de soluciones de Frobenius de
x2(2 − x2)y′′ − 2x(1 + 2x2)y′ + (2 − 2x2)y = 0. (9.7.6.21)
Dé fórmulas explícitas para los coeficientes en las soluciones.
Solución:
Para (9.7.6.21), los polinomios definidos en el Teorema 9.7.6.1 son
Como en la Sección 9.7.5, dado que p1 ≡ 0, las fórmulas de recurrencia del Teorema 9.7.6.1 implican que an(r) = 0 si n es impar, y
Dado que r1 = 1 es una raíz repetida del polinomio indicial p0, el Teorema 9.7.6.2 implica que
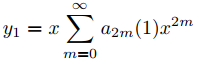(9.7.6.22)
y
(9.7.6.23)
forman un conjunto fundamental de soluciones de Frobenius de (9.7.6.21). Te dejamos a ti demostrar que
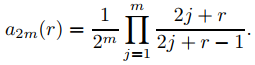(9.7.6.24)
Establecer r = 1 produce
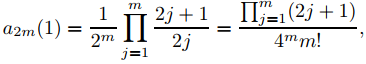(9.7.6.25)
y sustituyendo esto en (9.7.6.22) se obtiene
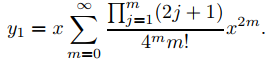
Para obtener y2 en (9.7.6.23), debemos calcular a′2m(1) para m = 1, 2, … Nuevamente usamos diferenciación logarítmica. De (9.7.6.24),
Tomando logaritmos, obtenemos
Derivando con respecto a r, se obtiene
Por lo tanto
Haciendo r = 1 y recordando (9.7.6.25), se obtiene
(9.7.6.26)
Dado que
(9.7.6.26) se puede reescribir como
Sustituyendo esto en (9.7.6.23) se obtiene
♦
Si la solución y1 = y(x, r1) de Ly = 0 se reduce a una suma finita, entonces existe la dificultad de usar la diferenciación logarítmica para obtener los coeficientes {a′n(r1)} en la segunda solución. El siguiente ejemplo ilustra esta dificultad y muestra cómo superarla.
.
Ejemplo ilustrativo 9.7.6.4
Encuentre un conjunto fundamental de soluciones de Frobenius de
x2y′′ − x(5 − x)y′ + (9 − 4x)y = 0. (9.7.6.27)
Dé fórmulas explícitas para los coeficientes en las soluciones.
Solución:
Para (9.7.6.27) los polinomios definidos en el Teorema 9.7.6.1 son
Como r1 = 3 es un cero repetido del polinomio indicial p0, el Teorema 9.7.6.2 implica que
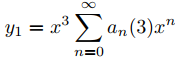(9.7.6.28)
y
(9.7.6.29)
son soluciones de Frobenius linealmente independientes de (9.7.6.27). Para encontrar los coeficientes en (7.6.28) usamos las fórmulas de recurrencia
Lo dejamos a usted para mostrar que
(9.7.6.30)
Establecer r = 3 aquí produce
entonces a1(3) = 1 y an(3) = 0 si n ≥ 2. Sustituyendo estos coeficientes en (9.7.6.28) se obtiene
y1 = x3(1 + x).
Para obtener y2 en (9.7.6.29) debemos calcular a′n(3) para n = 1, 2, . . . . Probemos primero la diferenciación logarítmica. De (9.7.6.30),
de esta manera
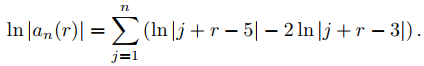
Derivando con respecto a r, se obtiene
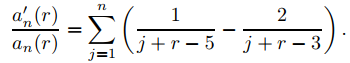
Por lo tanto
(9.7.6.31)
Sin embargo, no podemos simplemente establecer r = 3 aquí si n ≥ 2, ya que la expresión entre paréntesis en la suma correspondiente a j = 2 contiene el término 1/(r − 3). De hecho, dado que an(3) = 0 para n ≥ 2, la fórmula (9.7.6.31) para a′n(r) es en realidad una forma indeterminada en r = 3.
Superamos esta dificultad de la siguiente manera. De (9.7.6.30) con n = 1,
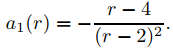
Por lo tanto
esto es
a’1(3) = −3. (9.7.6.32)
De (9.7.6.30) con n ≥ 2,
donde
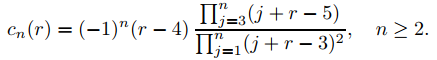
Por lo tanto
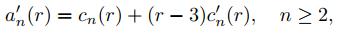
lo que implica que a′n(3) = cn(3) si n ≥ 3. Te dejamos comprobar que
Sustituyendo esto y (9.7.6.32) en (9.7.6.29) se obtiene
♦