| 9. Ecuaciones diferenciales | 9.8. La transformada de Laplace | Ejercicios propuestos para el Capítulo 9.8.4 |
9.8.4 La función escalón unitario
En la siguiente sección consideraremos problemas de valor inicial
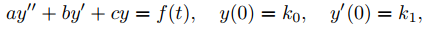
donde a, b y c son constantes y f es continua por tramos. En esta sección desarrollaremos procedimientos para usar la tabla de transformadas de Laplace para encontrar las transformadas de Laplace de funciones continuas por partes y para encontrar las inversas continuas por partes de las transformadas de Laplace.
Ejemplo 9.8.4.1
Utilice la tabla de transformadas de Laplace para encontrar la transformada de Laplace de
(9.8.4.1)
Figura 9.8.4.1 La función continua por tramos (9.8.4.1)
Solución:
Dado que la fórmula para f cambia en t = 2, escribimos
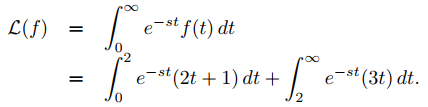(9.8.4.2)
Para relacionar el primer término con una transformada de Laplace, sumamos y restamos
en (9.8.4.2) para obtener
(9.8.4.3)
Para relacionar la última integral con una transformada de Laplace, hacemos el cambio de variable x = t − 2 y reescribimos la integral como
Dado que el símbolo utilizado para la variable de integración no tiene efecto sobre el valor de una integral definida, ahora podemos reemplazar x por la t más estándar y escribir
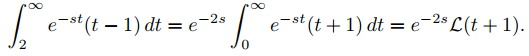
Esto y (9.8.4.3) implican que
Ahora podemos usar la tabla de transformadas de Laplace para encontrar que
♦
Transformadas de Laplace de funciones continuas por tramos
Ahora desarrollaremos el método del ejemplo 9.8.4.1 en una forma sistemática para encontrar la transformada de Laplace de una función continua por tramos. Es conveniente introducir la función escalón unitario, definida como
(9.8.4.4)
Por lo tanto, u(t) “pasa” del valor constante 0 al valor constante 1 en t = 0. Si reemplazamos t por t − τ en (9.8.4.4), entonces
es decir, el paso ahora ocurre en t = τ (Figura 9.8.4.2).
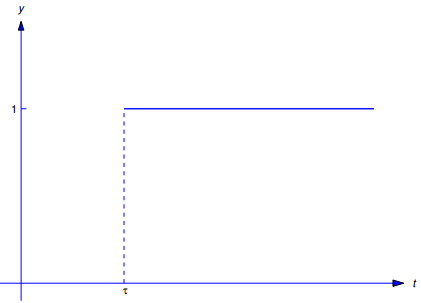
Figura 9.8.4.2 y = u(t − τ)
La función escalonada nos permite representar convenientemente funciones continuas por partes (tramos). Por ejemplo, considere la función
(9.8.4.5)
donde suponemos que f0 y f1 están definidas en [0, ∞), aunque son iguales a f solo en los intervalos indicados. Esta suposición nos permite reescribir (9.8.4.5) como
(9.8.4.6)
Para verificar esto, observe que si t < t1 entonces u(t − t1) = 0 y (9.8.4.6) se convierte en
Si t ≥ t1 entonces u(t − t1) = 1 y (9.8.4.6) se convierte en
Necesitamos el siguiente teorema para mostrar cómo se puede usar (9.8.4.6) para encontrar L(f)
Teorema 9.8.4.1
Sea g definida en [0, ∞). Supongamos que τ ≥ 0 y L(g(t + τ)) existe para s > s0. Entonces L(u(t − τ)g(t)) existe para s > s0, y
♦
Prueba:
Por definición,
De esto y de la definición de u(t − τ),
La primera integral a la derecha es igual a cero. Introduciendo la nueva variable de integración x = t − τ en la segunda integral se obtiene
Cambiando el nombre de la variable de integración en la última integral de x a t se obtiene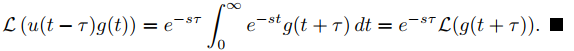
Ejemplo 9.8.4.2
Encontrar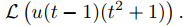
Solución:
Aquí τ = 1 y g(t) = t2 + 1, entonces
Ya que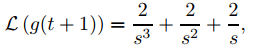
El teorema 9.8.4.1 implica que
♦
Ejemplo 9.8.4.3
Use el Teorema 9.8.4.1 para encontrar la transformada de Laplace de la función
del Ejemplo 9.8.4.1.
Solución:
Primero escribimos f en la forma (9.8.4.6) como
f(t) = 2t + 1 + u(t − 2)(t − 1).
Por lo tanto
que es el resultado obtenido en el ejemplo 9.8.4.1. ♦
La fórmula (9.8.4.6) puede extenderse a funciones continuas por tramos más generales. Por ejemplo, podemos escribir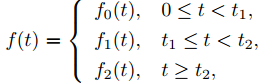
como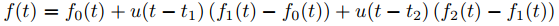
si f0, f1 y f2 están todas definidas en [0, ∞).
Ejemplo 9.8.4.4
Encuentre la transformada de Laplace de
(9.8.4.7)
Figura 9.8.4.3 La función continua por tramos (9.8.4.7)
Solución:
En términos de funciones escalonadas,
o
Ahora el Teorema 9.8.4.1 implica que
♦
Las identidades trigonométricas
sen(A + B) = senA cosB + cosA senB (9.8.4.8)
cos(A + B) = cosA cosB − senA senB (9.8.4.9)
son útiles en problemas que implican cambiar los argumentos de funciones trigonométricas. Usaremos estas identidades en el siguiente ejemplo.
Ejemplo 9.8.4.5
Encuentre la transformada de Laplace de
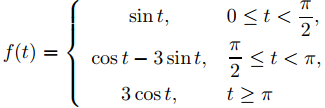(9.8.4.10)
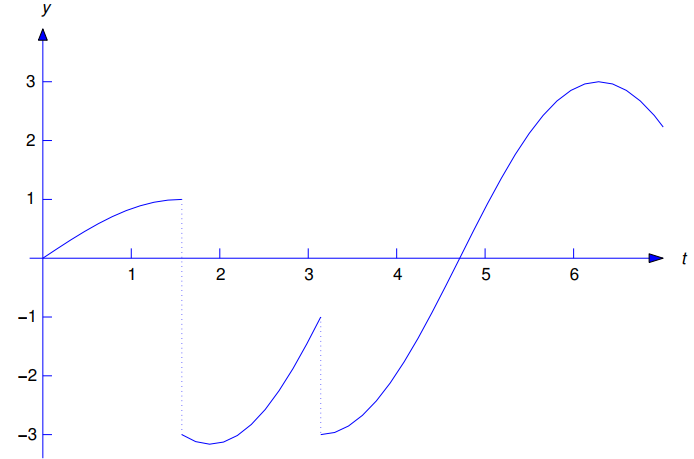
Figura 9.8.4.4 La función continua por tramos (9.8.4.10)
Solución:
En términos de funciones escalonadas,
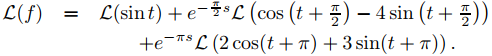(9.8.4.11)
Ya que
y
vemos de (9.8.4.11) que
♦
El segundo teorema de traslación
Reemplazando g(t) por g(t − τ) en el Teorema 9.8.4.1 se obtiene el siguiente teorema.
Teorema 9.8.4.2 Segundo teorema de traslación
Si τ ≥ 0 y L(g) existe para s > s0 entonces L(u(t − τ)g(t − τ)) existe para s > s0 y
o equivalente
(9.8.4.12) ♦
OBSERVACIÓN: Recuerde que el Primer Teorema del Desplazamiento (Teorema 9.8.1.3) establece que multiplicar una función por eat corresponde a desplazar el argumento de su transformada por a unidades. El Teorema 9.8.4.2 establece que multiplicar una transformada de Laplace por la exponencial e−τs corresponde a desplazando el argumento de la transformada inversa en τ unidades.
Ejemplo 9.8.4.6
Usa (9.8.4.12) para encontrar
Solución:
Para aplicar (9.8.4.12) hacemos τ = 2 y G(s) = 1/s2. Entonces g(t) = t y (9.8.4.12) implica que
♦
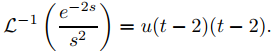Ejemplo 9.8.4.7
Encuentre la transformada inversa de Laplace h de
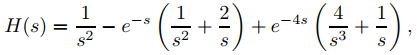
y encuentre fórmulas distintas para h en intervalos apropiados.
Solución:
Sea
Entonces
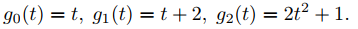
Por tanto, (9.8.4.12) y la linealidad de L−1 implican que
que también se puede escribir como
♦
Ejemplo 9.8.4.8
Encuentre la transformada inversa de
Solución:
Sea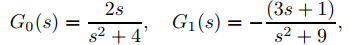
y
Entonces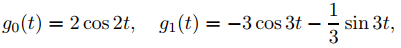
y
Por tanto (9.8.4.12) y la linealidad de L−1 implican que
Usando las identidades trigonométricas (9.8.4.8) y (9.8.4.9), podemos reescribir esto como
(9.8.4.13)
♦
Figura 9.8.4.5 La función continua por tramos (9.8.4.13)