| 6. Aplicaciones de la integral | Ejercicios propuestos del Capítulo 6.4 |
6.4 Longitud de arco de una curva y área de una superficie
Objetivos de aprendizaje:
6.4.1. Determinar la longitud de una curva, y = f (x), entre dos puntos.
6.4.2. Determinar la longitud de una curva, x = g (y), entre dos puntos.
6.4.3. Encontrar el área de superficie de un sólido de revolución.
En esta sección, usamos integrales definidas para encontrar la longitud del arco de una curva. Podemos pensar en la longitud del arco como la distancia que viajarías si estuvieras caminando por el camino de la curva. Muchas aplicaciones del mundo real implican la longitud del arco. Si se lanza un cohete a lo largo de una trayectoria parabólica, es posible que queramos saber qué tan lejos viaja el cohete. O, si una curva en un mapa representa un camino, es posible que deseemos saber qué tan lejos tenemos que conducir para llegar a nuestro destino.
Comenzamos calculando la longitud del arco de las curvas definidas como funciones de x, luego examinamos el mismo proceso para las curvas definidas como funciones de y. (El proceso es idéntico, con los roles de x e y invertidos). Las técnicas que usamos para hallar la longitud del arco se pueden extender para calcular el área de una superficie de revolución, y cerramos la sección con un examen de este concepto.
6.4.1 Longitud de arco de la curva y = f (x)
En aplicaciones anteriores de integración, requeríamos que la función f (x) fuera integrable, o al menos continua. Sin embargo, para calcular la longitud de arco tenemos un requisito más estricto para f(x). Ahora, requerimos que f(x) sea diferenciable, y además que su derivada, f ‘(x), sea continua. Las funciones como esta, que tienen derivadas continuas, se denominan suaves. (Esta propiedad vuelve a aparecer en capítulos posteriores).
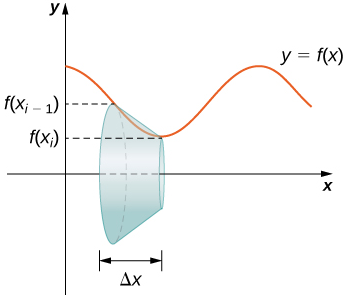
Sea f(x) una función suave definida sobre [a, b]. Queremos calcular la longitud de la curva desde el punto (a, f (a)) hasta el punto (b, f (b)). Comenzamos usando segmentos de recta para aproximar la longitud de la curva. Para i = 0, 1, 2, …, n, sea P = {xi} una partición regular de [a, b]. Luego, para i = 1, 2, …, n, se construye un segmento de recta desde el punto (xi − 1, f(xi − 1)) hasta el punto (xi, f(xi)). Aunque parezca lógico usar segmentos de recta horizontales o verticales, queremos que nuestros segmentos de recta se aproximen a la curva lo más posible. La figura 6.4.1 muestra esta construcción para n = 5.

Para auxiliarnos en el cálculo de la longitud de cada segmento de recta, observamos el cambio en la distancia vertical, así como el cambio en la distancia horizontal en cada intervalo. Como hemos usado una partición regular, el cambio en la distancia horizontal en cada intervalo viene dado por Δx. Sin embargo, el cambio en la distancia vertical varía de un intervalo a otro, por lo que usamos Δyi = f(xi) − f(xi − 1) para representar el cambio en la distancia vertical durante el intervalo [xi − 1, xi], como se muestra en Figura 6.4.2. Tenga en cuenta que algunos (o todos) los Δyi pueden ser negativos.

Según el teorema de Pitágoras, la longitud del segmento de recta es

También podemos escribir esto como

Ahora, según el teorema del valor medio, hay un punto xi* ∈ [xi − 1, xi] tal que f ′ (xi*) = (Δyi) / (Δx). Entonces la longitud del segmento de recta viene dada por

Sumando las longitudes de todos los segmentos de recta, obtenemos la siguiente aproximación para la longitud del arco

Esta es una suma de Riemann. Tomando el límite cuando n → ∞, obtenemos

Resumimos estos hallazgos en el siguiente teorema.
Teorema 6.4.1. Longitud del arco para y = f (x)
Sea f (x) una función suave en el intervalo cerrado [a, b]. Entonces, la longitud del arco de la porción de la gráfica de f (x) desde el punto (a, f (a)) hasta el punto (b, f (b)) viene dada por
Longitud de arco = \(\int_a^b \sqrt{1 + [f'(x)]^2} \, dx.\)
♦
Tenga en cuenta que estamos integrando una expresión que involucra f ′(x), por lo que debemos asegurarnos de que f ′(x) sea integrable. Es por eso que requerimos que f (x) sea suave.
Ejemplo ilustrativo 6.4_1: Cálculo de la longitud de arco de una función de x
Sea f (x)=2x3/2. Calcula la longitud del arco de la gráfica de f (x) sobre el intervalo [0, 1]. Redondea la respuesta a tres decimales.
Solución:
Tenemos f ′(x) = 3x1/2, entonces [f ′(x)]2 = 9x. Entonces, la longitud del arco es

Se sustituye u = 1 + 9x, entonces, du = 9dx. Cuando x = 0, entonces u = 1, y cuando x = 1, entonces u =10. Por lo tanto,
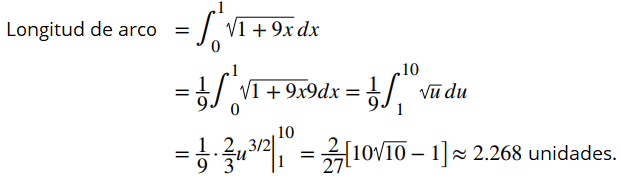
♦
Ejercicio de control 6.4.1
Sea \(f(x) = (4/3) x^{3/2}\). Calcule la longitud de arco de la gráfica de \(f(x)\) sobre el intervalo \([0, 1]\). Redondee la respuesta a tres lugares decimales. ♦
Aunque es bueno tener una fórmula para calcular la longitud del arco, este teorema particular puede generar expresiones que son difíciles de integrar. Estudiamos algunas técnicas para la integración en Introducción a las técnicas de integración. En algunos casos, es posible que tengamos que usar una computadora o una calculadora para aproximar el valor de la integral.
Ejemplo ilustrativo 6.4_2: Uso de una computadora o calculadora para determinar la longitud de arco de una función de x
Sea \(f(x) = x^2\). Calcule la longitud de arco de la gráfica de \(f(x)\) sobre el intervalo \([1, 3]\).
Solución:
Tenemos \(f'(x) = 2x\), así que \([f'(x)]^2 = 4x^2\). Entonces, la longitud de arco está dada por
Longitud de arco = \(\int_a^b \sqrt{1 + [f'(x)]^2} \, dx = \int_1^3 \sqrt{1 + 4x^2} \, dx\).
Usando una computadora para aproximar el valor de esta integral, obtenemos
\(\int_1^3 \sqrt{1 + 4x^2} \, dx \approx 8.26815\).
♦
Ejercicio de control 6.4.2
Sea \(f(x) = \sin x\). Calcule la longitud de arco de la gráfica de \(f(x)\) sobre el intervalo \([0, \pi]\). Use una computadora o calculadora para aproximar el valor de la integral. ♦
Longitud del arco de la curva x = g(y)
Acabamos de ver cómo aproximar la longitud de una curva con segmentos de recta. Si queremos encontrar la longitud del arco de la gráfica de una función de y, podemos repetir el mismo proceso, excepto que dividimos el eje y en lugar del eje x. La figura 6.4.3 muestra un segmento de recta representativo.

Tenemos que la longitud del segmento de recta es

que también se puede escribir como

Si ahora seguimos el mismo desarrollo que hicimos anteriormente, obtenemos una fórmula para la longitud del arco de una función x = g(y).
Teorema 6.4.2. Longitud del arco para x = g(y)
Sea g(y) una función suave en un intervalo cerrado [c, d]. Entonces, la longitud del arco de la gráfica de g(y) desde el punto (c, g(c)) hasta el punto (d, g(d)) viene dada por
Longitud de arco = \(\int_c^d \sqrt{1 + [g'(y)]^2} \, dy.\)
♦
Ejemplo ilustrativo 6.4_3: Calculando la longitud de arco de una función de y
Sea \(g(y) = 3y^3\). Calcule la longitud de arco de la gráfica de \(g(y)\) sobre el intervalo \([1, 2]\).
Solución:
Tenemos \(g'(y) = 9y^2\), así que \([g'(y)]^2 = 81y^4\). Entonces, la longitud de arco es
Longitud de arco = \(\int_c^d \sqrt{1 + [g'(y)]^2} \, dy = \int_1^2 \sqrt{1 + 81y^4} \, dy\).
Usando una computadora para aproximar el valor de esta integral, obtenemos
\(\int_1^2 \sqrt{1 + 81y^4} \, dy \approx 21.0277\).
♦
Ejercicio de control 6.4.3
Sea \(g(y) = 1/y\). Calcule la longitud de arco de la gráfica de \(g(y)\) sobre el intervalo \([1, 4]\). Use una computadora o calculadora para aproximar el valor de la integral. ♦
Área de una superficie de revolución
Los conceptos que usamos para encontrar la longitud de arco de una curva se pueden extender para encontrar el área de superficie de una superficie de revolución. El área de superficie es el área total de la capa externa de un objeto. Para objetos como cubos o ladrillos, por ejemplo, la superficie del objeto es la suma de las áreas de todas sus caras. Para superficies curvas, la situación es un poco más compleja. Sea f(x) una función suave no negativa en el intervalo cerrado [a, b]. Deseamos encontrar el área de la superficie de la revolución creada al girar la gráfica de y = f(x) alrededor del eje x como se muestra en la siguiente figura.

Como lo hemos hecho muchas veces antes, vamos a dividir el intervalo [a, b] y aproximar el área de superficie calculando el área de superficie de formas más simples. Comenzamos usando segmentos de recta para aproximar la curva, como lo hicimos anteriormente en esta sección. Para i = 0, 1, 2, …, n, sea P = {xi} una partición regular de [a, b]. Luego, para i = 1, 2, …, n, se construye un segmento de recta desde el punto (xi − 1, f(xi − 1)) hasta el punto (xi, f(xi)). Ahora, giramos estos segmentos de recta alrededor del eje x para generar una aproximación de la superficie de revolución como se muestra en la siguiente figura.

Para calcular el área de superficie de la banda, necesitamos encontrar el área de superficie lateral, S, del tronco (el área de solo la superficie exterior inclinada del tronco, sin incluir las áreas de las caras superior o inferior). Sean r1 y r2 los radios del extremo ancho y el extremo estrecho del tronco, respectivamente, y sea l la altura inclinada del tronco como se muestra en la siguiente figura.

Sabemos que la superficie lateral de un cono está dada por
Área de superficie lateral = πrs,
donde r es el radio de la base del cono y s es la altura inclinada (vea la siguiente figura).
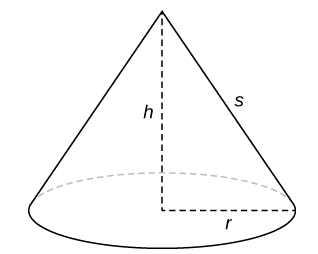
Dado que un tronco puede considerarse como una pieza de un cono, el área de la superficie lateral del tronco está dada por el área de la superficie lateral de todo el cono menos el área de la superficie lateral del cono más pequeño (la parte puntiaguda) que se cortó (ver la siguiente figura).

Las secciones transversales del cono pequeño y el cono grande son triángulos semejantes, por lo que vemos que

Resolviendo para s, obtenemos
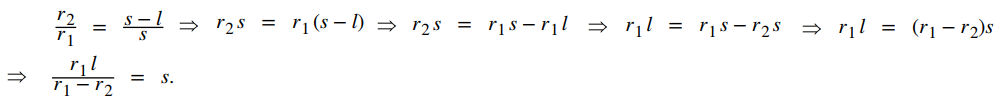
Entonces el área de superficie lateral (SA) del tronco es

Ahora usemos esta fórmula para calcular el área de superficie de cada una de las bandas formadas al girar los segmentos de recta alrededor del eje x. Una banda representativa se muestra en la siguiente figura.
Tenga en cuenta que la altura inclinada de este tronco es solo la longitud del segmento de recta utilizado para generarlo. Entonces, aplicando la fórmula del área de superficie, tenemos
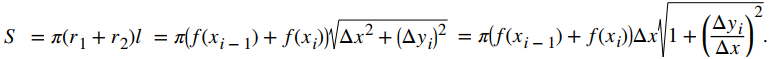
Ahora, como lo hicimos en el desarrollo de la fórmula de longitud de arco, aplicamos el Teorema del valor medio para seleccionar xi* ∈ [xi − 1, xi] de modo que f ′ (xi*) = (Δyi) / Δx. Esto nos da

Además, dado que f (x) es continua, según el Teorema del valor medio, hay un punto xi** ∈ [xi − 1, xi] tal que f (xi**) = (1/2) [f(xi − 1) + f(xi)], entonces obtenemos
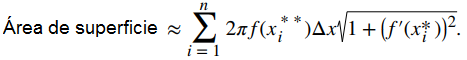
Esto casi parece una suma de Riemann, excepto que tenemos funciones evaluadas en dos puntos diferentes, xi* y xi** en el intervalo [xi − 1, xi]. Aunque no examinamos los detalles aquí, resulta que debido a que f (x) es suave, si dejamos n → ∞, el límite funciona igual que una suma de Riemann incluso con los dos puntos de evaluación diferentes. Esto tiene sentido intuitivamente. Tanto xi* como xi** están en el intervalo[xi − 1, xi], por lo que tiene sentido que cuando n → ∞, tanto xi* como xi** tienda a x. Aquellos de ustedes que estén interesados en los detalles deben consultar un texto de cálculo avanzado.
Tomando el límite cuando n → ∞, obtenemos

Al igual que con la longitud del arco, podemos realizar un desarrollo similar para las funciones de y para obtener una fórmula para el área de superficie de las superficies de revolución alrededor del eje y. Estos hallazgos se resumen en el siguiente teorema.
Teorema 6.4.3. Área superficial de una superficie de revolución
Sea f(x) una función suave no negativa en el intervalo cerrado [a, b]. Entonces, el área superficial de la superficie de revolución formada al girar la gráfica de f(x) alrededor del eje x viene dada por
Área de una superficie = \(\int_a^b (2\pi f(x) \sqrt{1 + (f'(x))^2})\, dx.\)
Del mismo modo, sea g(y) una función suave no negativa en el intervalo cerrado [c, d]. Entonces, el área superficial de la superficie de revolución formada al girar la gráfica de g(y) entorno del eje y viene dada por
Área de una superficie = \(\int_c^d (2\pi g(y) \sqrt{1 + (g'(y))^2})\, dy.\)
♦
Ejemplo ilustrativo 6.4_4: Calculando el área de la superficie de un sólido de revolución 1
Sea \( f(x) = \sqrt{x} \) sobre el intervalo \([1, 4]\). Encuentre el área de la superficie del sólido generado al rotar la gráfica de \( f(x) \) alrededor del eje x. Redondee la respuesta a tres decimales.
Solución:
El gráfico de f (x) y la superficie de rotación se muestran en la siguiente figura.
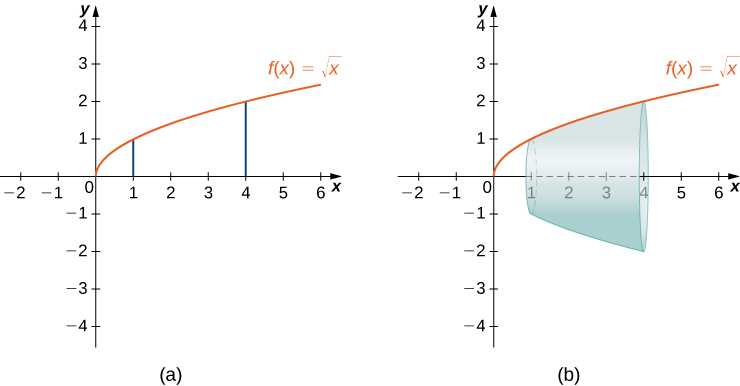
Figura 6.4.9 (a) El gráfico de f (x). (b) La superficie de revolución.
Tenemos \(f(x) = \sqrt{x}\). Entonces, \(f'(x) = 1/(2\sqrt{x})\) y \((f'(x))^2 = 1/(4x)\). Entonces,
Área de la superficie = \(\int_a^b (2\pi f(x) \sqrt{1 + (f'(x))^2})\, dx\)
= \(\int_1^4 (2\pi \sqrt{x} \sqrt{1 + \frac{1}{4x}})\, dx\)
= \(\int_1^4 (2\pi \sqrt{x + \frac{1}{4}})\, dx\).
Sea \(u = x + 1/4\). Entonces, \(du = dx\). Cuando \(x = 1\), \(u = 5/4\), y cuando \(x = 4\), \(u = 17/4\). Esto nos da
\(\int_1^4 (2\pi \sqrt{x + \frac{1}{4}})\, dx\) = \(\int_{5/4}^{17/4} 2\pi \sqrt{u}\, du\)
= \(2\pi [\frac{2}{3}u^{3/2}]_{5/4}^{17/4} = \frac{\pi}{6}[17\sqrt{17} – 5\sqrt{5}] \approx 30.846\).
♦
Ejercicio de control 6.4.4
Sea \( f(x) = \sqrt{1 – x} \) sobre el intervalo \([0, 1/2]\). Encuentre el área de la superficie del sólido generado al rotar la gráfica de \( f(x) \) alrededor del eje x. Redondee la respuesta a tres decimales. ♦
Ejemplo ilustrativo 6.4_5: Calculando el área de la superficie de un sólido de revolución 2
Sea \(f(x) = y = \sqrt[3]{3x}\). Considere la porción de la curva donde \(0 \leq y \leq 2\). Encuentre el área de la superficie del sólido generado al rotar la gráfica de \(f(x)\) alrededor del eje y.
Solución:
Note que estamos rotando la curva alrededor del eje y, y el intervalo está en términos de y, así que queremos reescribir la función como una función de y. Obtenemos \(x = g(y) = (1/3)y^3\). La gráfica de \(g(y)\) y la superficie de rotación se muestran en la siguiente figura.
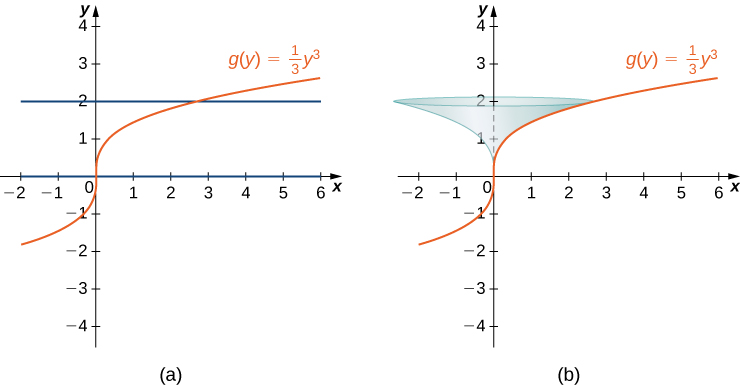
Figura 6.4.10 (a) El gráfico de g(y). (b) La superficie de revolución.
Tenemos \(g(y) = (1/3)y^3\), así que \(g'(y) = y^2\) y \((g'(y))^2 = y^4\). Entonces,
Área de la superficie = \(\int_c^d (2\pi g(y) \sqrt{1 + (g'(y))^2})\, dy\)
= \(\int_0^2 (2\pi (\frac{1}{3}y^3) \sqrt{1 + y^4})\, dy\)
= \(\frac{2\pi}{3} \int_0^2 (y^3 \sqrt{1 + y^4})\, dy\).
Sea \(u = y^4 + 1\). Entonces \(du = 4y^3\, dy\). Cuando \(y = 0\), \(u = 1\), y cuando \(y = 2\), \(u = 17\). Entonces
\(\frac{2\pi}{3} \int_0^2 (y^3 \sqrt{1 + y^4})\, dy = \frac{2\pi}{3} \int_1^{17} \frac{1}{4}\sqrt{u}\, du\)
= \(\frac{\pi}{6} [\frac{2}{3}u^{3/2}]_1^{17} = \frac{\pi}{9} [(17)^{3/2} – 1] \approx 24.118\).
♦
Ejercicio de control 6.4.5
Sea \( g(y) = \sqrt{9 – y^2} \) sobre el intervalo \(y \in [0, 2]\). Encuentre el área de la superficie del sólido generado al rotar la gráfica de \( g(y) \) alrededor del eje y. ♦

No están los ejercicios resueltos
Hola Rafael. Gracias por el comentario. Todavía no he publicado los ejercicios. Los ejercicios propuestos los tomo del libro de Calculo de OpenStax y los resueltos del libro de Zill. En estos días voy a publicar ejemplos ilustrativos 😺👀
I got this site from my pal who informed me on the topic of this web
site and at the moment this time I am visiting this web site
and reading very informative articles here.
Es notable para mí tener a la mano un sitio web que es útil para apoyar mi conocimiento en esta rama de la matemática. Gracias administrador
When someone writes an post he/she maintains the image of a user in his/her mind that how
a user can be aware of it. Therefore that’s
why this post is perfect. Thanks!