Ejercicios propuestos para el capítulo 10.15
Para los siguientes ejercicios, evalúe las integrales de línea aplicando el teorema de Green.
146. \(\displaystyle \int_C 2xy\,dx + (x + y)\,dy\), donde \( C \) es el camino desde \((0, 0)\) hasta \((1, 1)\) a lo largo de la gráfica de \( y = x^3 \) y desde \((1, 1)\) hasta \((0, 0)\) a lo largo de la gráfica de \( y = x \) orientado en dirección contraria a las manecillas del reloj.
147. \(\displaystyle \int_C 2xy\,dx + (x + y)\,dy\), donde \( C \) es el límite de la región que se encuentra entre las gráficas de \( y = 0 \) y \( y = 4 – x^2 \) orientado en dirección contraria a las manecillas del reloj.
148. \(\displaystyle \int_C 2 \arctan \left( \frac{y}{x} \right) dx + \ln \left( x^2 + y^2 \right) dy\), donde \( C \) está definido por \( x = 4 + 2 \cos \theta, y = 4 \sin \theta \) orientado en dirección contraria a las manecillas del reloj.
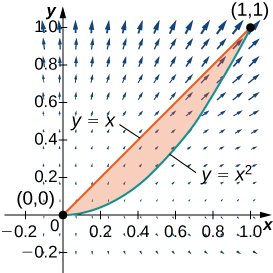
149. \(\displaystyle \int_C \sin x \cos y\,dx + (xy + \cos x \sin y)\,dy\), donde \( C \) es el límite de la región que se encuentra entre las gráficas de \( y = x \) y \( y = \sqrt{x} \) orientado en dirección contraria a las manecillas del reloj.
150. \(\displaystyle \int_C xy\,dx + (x + y)\,dy\), donde \( C \) es el límite de la región que se encuentra entre las gráficas de \( x^2 + y^2 = 1 \) y \( x^2 + y^2 = 9 \) orientado en dirección contraria a las manecillas del reloj.
151. \(\displaystyle \int_C (-y\,dx + x\,dy)\), donde \( C \) consiste en el segmento de línea \( C_1 \) desde \((-1, 0)\) hasta \((1, 0)\), seguido por el arco semicircular \( C_2 \) desde \((1, 0)\) de regreso a \((-1, 0)\).
Para los siguientes ejercicios, use el teorema de Green.
152. Sea \( C \) la curva que consiste en segmentos de línea desde \((0, 0)\) hasta \((1, 1)\), luego hasta \((0, 1)\) y de regreso a \((0, 0)\). Encuentre el valor de \(\displaystyle \int_C xy\,dx + \sqrt{y^2 + 1}\,dy\).
153. Evalúe la integral de línea \(\displaystyle \int_C x e^{-2x}\,dx + (x^4 + 2x^2 y^2)\,dy\), donde \(C\) es el límite de la región entre los círculos \(x^2 + y^2 = 1\) y \(x^2 + y^2 = 4\), y es una curva orientada positivamente.
154. Encuentre la circulación en sentido contrario a las manecillas del reloj del campo \(F(x, y) = xy\,i + y^2\,j\) alrededor y sobre el límite de la región encerrada por las curvas \(y = x^2\) y \(y = x\) en el primer cuadrante y orientada en dirección contraria a las manecillas del reloj.
155. Evalúe \(\displaystyle \int_C y^3\,dx – x^3 y^2\,dy\), donde \( C \) es el círculo de radio 2 centrado en el origen con orientación positiva.
156. Evalúe \(\displaystyle \int_C y^3\,dx – x^3\,dy\), donde \( C \) incluye los dos círculos de radio 2 y radio 1 centrados en el origen, ambos con orientación positiva.
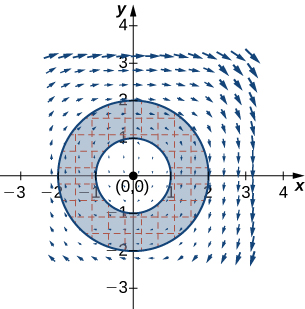
157. Calcule \(\displaystyle \int_C -x^2 y\,dx + x y^2\,dy\), donde \( C \) es un círculo de radio 2 centrado en el origen y orientado en dirección contraria a las manecillas del reloj.
158. Calcule la integral \(\displaystyle \int_C 2[y + x \sin(y)] \, dx + [x^2 \cos(y) – 3y^2] \, dy\) a lo largo del triángulo \( C \) con vértices \((0, 0)\), \((1, 0)\) y \((1, 1)\), orientado en dirección contraria a las manecillas del reloj, utilizando el teorema de Green.
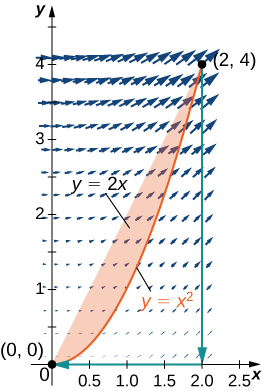
159. Evalúe la integral \(\displaystyle \int_C (x^2 + y^2) \, dx + 2xy\,dy\), donde \( C \) es la curva que sigue la parábola \(\displaystyle y = x^2\) desde \((0, 0)\) hasta \((2, 4)\), luego la línea desde \((2, 4)\) hasta \((2, 0)\), y finalmente la línea desde \((2, 0)\) hasta \((0, 0)\).
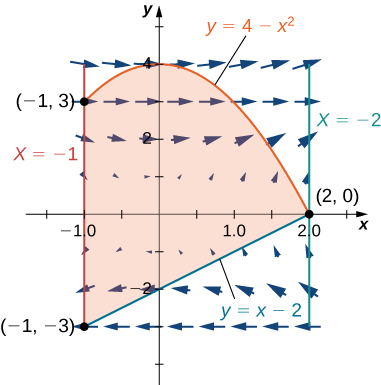
160. Evalúe la integral de línea \(\displaystyle \int_C (y – \sin(y) \cos(y))\,dx + 2x \sin^2(y)\,dy\), donde \( C \) es una trayectoria orientada en dirección contraria a las manecillas del reloj alrededor de la región delimitada por \( x = -1 \), \( x = 2 \), \( y = 4 – x^2 \) y \( y = x – 2 \).
Para los siguientes ejercicios, use el teorema de Green para encontrar el área.
161. Encuentre el área entre la elipse \(\displaystyle \frac{x^2}{9} + \frac{y^2}{4} = 1\) y el círculo \(\displaystyle x^2 + y^2 = 25\).
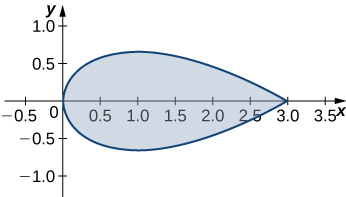
162. Encuentre el área de la región encerrada por la ecuación paramétrica
\[ p(\theta) = (\cos(\theta) – \cos^2(\theta)) \, i + (\sin(\theta) – \cos(\theta)\sin(\theta)) \, j \text{ para } 0 \leq \theta \leq 2\pi. \]
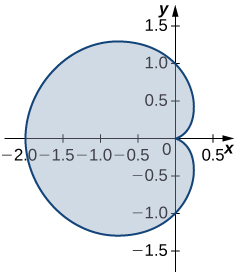
163. Encuentre el área de la región acotada por la hipocicloide \(\displaystyle r(t) = \cos^3(t)\,i + \sin^3(t)\,j\). La curva está parametrizada por \(\displaystyle t \in [0, 2\pi]\).
164. Encuentre el área de un pentágono con vértices \(\displaystyle (0, 4), (4, 1), (3, 0), (-1, -1)\) y \(\displaystyle (-2, 2)\).
165. Use el teorema de Green para evaluar \(\displaystyle \int_{C^+} (y^2 + x^3) \, dx + x^4 \, dy\), donde \(\displaystyle C^+\) es el perímetro del cuadrado \(\displaystyle [0, 1] \times [0, 1]\) orientado en sentido contrario a las manecillas del reloj.
166. Use el teorema de Green para demostrar que el área de un disco con radio \(\displaystyle a\) es \(\displaystyle A = \pi a^2\).
167. Use el teorema de Green para encontrar el área de un lazo de una rosa de cuatro hojas \(\displaystyle r = 3 \sin 20\). (Sugerencia: \(\displaystyle x\,dy – y\,dx = r^2 \,d\theta\).)
168. Use el teorema de Green para encontrar el área bajo un arco de la cicloide dada por las ecuaciones paramétricas \(\displaystyle x = t – \sin t, y = 1 – \cos t, t \geq 0\).
169. Use el teorema de Green para encontrar el área de la región encerrada por la curva
\[ r(t) = t^2 \,i + \left( \frac{t^3}{3} – t \right) \,j, \quad -\sqrt{3} \leq t \leq \sqrt{3}. \]
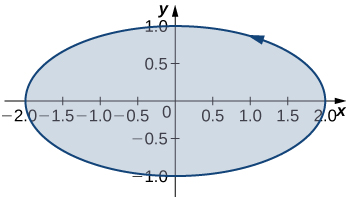
170. [T] Verifique el teorema de Green utilizando un sistema de álgebra computacional para evaluar la integral \(\displaystyle \int_C x e^y \, dx + e^x \, dy\), donde \(\displaystyle C\) es el círculo dado por \(\displaystyle x^2 + y^2 = 4\) y está orientado en dirección contraria a las manecillas del reloj.
171. Evalúe \(\displaystyle \int_C (x^2 y – 2xy + y^2) \, ds\), donde \(\displaystyle C\) es el límite del cuadrado unitario \(\displaystyle 0 \leq x \leq 1, \, 0 \leq y \leq 1,\) recorrido en sentido contrario a las manecillas del reloj. Use \(\displaystyle ds = dx + dy\) para este ejercicio.
172. Evalúe \(\displaystyle \int_C \frac{-(y+2)\,dx + (x-1)\,dy}{(x-1)^2 + (y+2)^2}\), donde \(\displaystyle C\) es cualquier curva cerrada simple cuyo interior no contiene el punto \(\displaystyle (1, -2)\) recorrida en sentido contrario a las manecillas del reloj.
173. Evalúe \(\displaystyle \int_C \frac{x\,dx + y\,dy}{x^2 + y^2}\), donde \(\displaystyle C\) es cualquier curva cerrada simple, suave y por partes que encierra el origen, recorrida en sentido contrario a las manecillas del reloj.
Para los siguientes ejercicios, use el teorema de Green para calcular el trabajo realizado por la fuerza \(\displaystyle F\) sobre una partícula que se mueve en sentido contrario a las manecillas del reloj alrededor de la trayectoria cerrada \(\displaystyle C\).
174. \(\displaystyle F(x, y) = xy\mathbf{i} + (x + y)\mathbf{j}, \, C : x^2 + y^2 = 4\)
175. \(\displaystyle F(x, y) = (x^{3/2} – 3y)\mathbf{i} + (6x + 5\sqrt{y})\mathbf{j}, \, C : \text{límite de un triángulo con vértices } (0, 0), (5, 0), \text{ y } (0, 5)\)
176. Evalúe \(\displaystyle \int_C (2x^3 – y^3) \, dx + (x^3 + y^3) \, dy\), donde \(\displaystyle C\) es un círculo unitario orientado en dirección contraria a las manecillas del reloj.
177. Una partícula comienza en el punto \(\displaystyle (-2, 0)\), se mueve a lo largo del eje \(\displaystyle x\) hasta \(\displaystyle (2, 0)\), y luego viaja a lo largo del semicírculo \(\displaystyle y = \sqrt{4 – x^2}\) hasta el punto de partida. Use el teorema de Green para encontrar el trabajo realizado sobre esta partícula por el campo de fuerza \(\displaystyle F(x, y) = x\mathbf{i} + (x^3 + 3xy^2)\mathbf{j}\).
178. David y Sandra patinan en un estanque sin fricción con viento. David patina por el interior, siguiendo un círculo de radio 2 en dirección contraria a las manecillas del reloj. Sandra patina una vez alrededor de un círculo de radio 3, también en dirección contraria a las manecillas del reloj. Suponga que la fuerza del viento en el punto \(\displaystyle (x, y)\) es \(\displaystyle F(x, y) = (x^2y + 10y)\mathbf{i} + (x^3 + 2xy^2)\mathbf{j}\). Use el teorema de Green para determinar quién realiza más trabajo.
179. Use el teorema de Green para encontrar el trabajo realizado por el campo de fuerza \(\displaystyle F(x, y) = (3y – 4x)\mathbf{i} + (4x – y)\mathbf{j}\) cuando un objeto se mueve una vez en sentido contrario a las manecillas del reloj alrededor de la elipse \(\displaystyle 4x^2 + y^2 = 4\).
180. Use el teorema de Green para evaluar la integral de línea \(\displaystyle \int_C e^{2x}\sin 2y \, dx + e^{2x}\cos 2y \, dy\), donde \(\displaystyle C\) es la elipse \(\displaystyle 9(x – 1)^2 + 4(y – 3)^2 = 36\) orientada en sentido contrario a las manecillas del reloj.
181. Evalúe la integral de línea \(\displaystyle \int_C y^2 \, dx + x^2 \, dy\), donde \(\displaystyle C\) es el límite de un triángulo con vértices \(\displaystyle (0, 0), (1, 1)\) y \(\displaystyle (1, 0)\), con orientación en sentido contrario a las manecillas del reloj.
182. Use el teorema de Green para evaluar la integral de línea \(\displaystyle \int_C \mathbf{h} \cdot d\mathbf{r}\) si \(\displaystyle \mathbf{h}(x, y) = e^{y} – \sin \pi x\), donde \(\displaystyle C\) es un triángulo con vértices \(\displaystyle (1, 0), (0, 1)\) y \(\displaystyle (-1, 0)\) recorrido en sentido contrario a las manecillas del reloj.
183. Use el teorema de Green para evaluar la integral de línea \(\displaystyle \int_C \sqrt{1 + x^3} \, dx + 2xy \, dy\) donde \(\displaystyle C\) es un triángulo con vértices \(\displaystyle (0, 0), (1, 0)\) y \(\displaystyle (1, 3)\) orientado en sentido horario.
184. Use el teorema de Green para evaluar la integral de línea \(\displaystyle \int_C x^2 y \, dx – xy^2 \, dy\) donde \(\displaystyle C\) es un círculo \(\displaystyle x^2 + y^2 = 4\) orientado en sentido contrario a las manecillas del reloj.
185. Use el teorema de Green para evaluar la integral de línea \(\displaystyle \int_C (3y – e^{\sin x}) \, dx + (7x + \sqrt{y^4 + 1}) \, dy\) donde \(\displaystyle C\) es un círculo \(\displaystyle x^2 + y^2 = 9\) orientado en sentido contrario a las manecillas del reloj.
186. Use el teorema de Green para evaluar la integral de línea \(\displaystyle \int_C (3x – 5y) \, dx + (x – 6y) \, dy\), donde \(\displaystyle C\) es una elipse \(\displaystyle \frac{x^2}{4} + y^2 = 1\) y está orientada en sentido contrario a las manecillas del reloj.
187. Sea \(\displaystyle C\) una curva triangular cerrada desde \(\displaystyle (0, 0)\) hasta \(\displaystyle (1, 0)\), luego hasta \(\displaystyle (1, 1)\) y finalmente de regreso a \(\displaystyle (0, 0)\). Sea
\[F(x, y) = 4y\mathbf{i} + 6x^2\mathbf{j}.\]
Use el teorema de Green para evaluar
\[\int_C F \cdot ds.\]
188. Use el teorema de Green para evaluar la integral de línea
\[\int_C y\,dx – x\,dy,\]
donde \(\displaystyle C\) es el círculo \(\displaystyle x^2 + y^2 = a^2\) orientado en sentido horario.
189. Use el teorema de Green para evaluar la integral de línea
\[\int_C (y + x)\,dx + (x + \sin y)\,dy,\]
donde \(\displaystyle C\) es cualquier curva cerrada simple y suave que une el origen consigo mismo, orientada en sentido contrario a las manecillas del reloj.
190. Use el teorema de Green para evaluar la integral de línea
\[\int_C \left(y – \ln (x^2 + y^2)\right) dx + \left(2 \arctan \frac{y}{x}\right) dy,\]
donde \(\displaystyle C\) es el círculo \(\displaystyle (x – 2)^2 + (y – 3)^2 = 1\) orientado positivamente.
191. Use el teorema de Green para evaluar
\[\int_C xy\,dx + x^3 y^3\,dy,\]
donde \(\displaystyle C\) es un triángulo con vértices \(\displaystyle (0, 0)\), \(\displaystyle (1, 0)\) y \(\displaystyle (1, 2)\) con orientación positiva.
192. Use el teorema de Green para evaluar la integral de línea
\[\int_C \sin y\,dx + x \cos y\,dy,\]
donde \(\displaystyle C\) es la elipse \(\displaystyle x^2 + xy + y^2 = 1\) orientada en sentido contrario a las manecillas del reloj.
193. Sea
\[F(x, y) = \left(\cos (x^5) – \frac{1}{3}y^3\right)\mathbf{i} + \frac{1}{3}x^3\mathbf{j}.\]
Encuentre la circulación en sentido contrario a las manecillas del reloj
\[\int_C F \cdot dr,\]
donde \(\displaystyle C\) es una curva que consiste en el segmento de línea que une \(\displaystyle (-2, 0)\) y \(\displaystyle (-1, 0)\), el semicírculo \(\displaystyle y = \sqrt{1 – x^2}\), el segmento de línea que une \(\displaystyle (1, 0)\) y \(\displaystyle (2, 0)\), y el semicírculo \(\displaystyle y = \sqrt{4 – x^2}\).
194. Use el teorema de Green para evaluar la integral de línea \(\displaystyle \int_C \sin \left( x^3 \right) dx + 2ye^{x^2} dy\), donde \(\displaystyle C\) es una curva triangular cerrada que conecta los puntos \(\displaystyle (0, 0)\), \(\displaystyle (2, 2)\) y \(\displaystyle (0, 2)\) en sentido contrario a las manecillas del reloj.
195. Sea \(\displaystyle C\) el límite del cuadrado \(\displaystyle 0 \leq x \leq \pi, 0 \leq y \leq \pi\), recorrido en sentido contrario a las manecillas del reloj. Use el teorema de Green para encontrar \(\displaystyle \int_C \sin \left( x + y \right) dx + \cos \left( x + y \right) dy\).
196. Use el teorema de Green para evaluar la integral de línea \(\displaystyle \int_C \mathbf{F} \cdot d\mathbf{r}\), donde \(\displaystyle \mathbf{F}(x, y) = \left( y^2 – x^2 \right) \mathbf{i} + \left( x^2 + y^2 \right) \mathbf{j}\), y \(\displaystyle C\) es un triángulo delimitado por \(\displaystyle y = 0, x = 3\) y \(\displaystyle y = x\), orientado en sentido contrario a las manecillas del reloj.
197. Use el teorema de Green para evaluar la integral \(\displaystyle \int_C \mathbf{F} \cdot d\mathbf{r}\), donde \(\displaystyle \mathbf{F}(x, y) = \left( xy^2 \right) \mathbf{i} + x\mathbf{j}\), y \(\displaystyle C\) es un círculo unitario orientado en sentido contrario a las manecillas del reloj.
198. Use el teorema de Green en un plano para evaluar la integral de línea \(\displaystyle \int_C \left( xy + y^2 \right) dx + x^2 dy\), donde \(\displaystyle C\) es una curva cerrada de una región delimitada por \(\displaystyle y = x\) y \(\displaystyle y = x^2\), orientada en sentido contrario a las manecillas del reloj.
199. Calcule el flujo hacia afuera de \(\displaystyle \mathbf{F} = -x\mathbf{i} + 2y\mathbf{j}\) sobre un cuadrado con esquinas \(\displaystyle (\pm 1, \pm 1)\), donde la normal unitaria apunta hacia afuera y está orientada en sentido contrario a las manecillas del reloj.
200. [T] Sea \(\displaystyle C\) el círculo \(\displaystyle x^2 + y^2 = 4\) orientado en sentido contrario a las manecillas del reloj. Evalúe \(\displaystyle \int_C \left[ \left( 3y – e^{\tan^{-1}x} \right) dx + \left( 7x + \sqrt{y^4 + 1} \right) dy \right]\) utilizando un sistema de álgebra computacional.
201. Encuentre el flujo del campo \(\displaystyle \mathbf{F} = -x\mathbf{i} + y\mathbf{j}\) a través de \(\displaystyle x^2 + y^2 = 16\) orientado en sentido contrario a las manecillas del reloj.
202. Sea \(\displaystyle \mathbf{F} = \left( y^2 – x^2 \right) \mathbf{i} + \left( x^2 + y^2 \right) \mathbf{j}\), y sea \(\displaystyle C\) un triángulo delimitado por \(\displaystyle y = 0, x = 3\) y \(\displaystyle y = x\), orientado en sentido contrario a las manecillas del reloj. Encuentre el flujo hacia afuera de \(\displaystyle \mathbf{F}\) a través de \(\displaystyle C\).
203. [T] Sea \(\displaystyle C\) el círculo unitario \(\displaystyle x^2 + y^2 = 1\) recorrido una vez en sentido contrario a las manecillas del reloj. Evalúe \[ \int_C \left[ -y^3 + \sin (xy) + xy \cos (xy) \right] dx + \left[ x^3 + x^2 \cos (xy) \right] dy \] utilizando un sistema de álgebra computacional.
204. [T] Encuentre el flujo hacia afuera del campo vectorial \(\displaystyle \mathbf{F} = xy^2 \mathbf{i} + x^2 y \mathbf{j}\) a través del límite del anillo \[ R = \{(x,y) : 1 \leq x^2 + y^2 \leq 4\} = \{(r,\theta) : 1 \leq r \leq 2, 0 \leq \theta \leq 2\pi\} \] utilizando un sistema de álgebra computacional.
205. Considere la región \(\displaystyle R\) delimitada por las parábolas \(\displaystyle y = x^2\) y \(\displaystyle x = y^2\). Sea \(\displaystyle C\) el límite de \(\displaystyle R\) orientado en sentido contrario a las manecillas del reloj. Use el teorema de Green para evaluar \[ \int_C \left( y + e^{\sqrt{x}} \right) dx + \left( 2x + \cos (y^2) \right) dy. \]
