| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.15 |
10.15 Teorema de Green
Objetivos de aprendizaje
10.15.1 Aplicar la forma de circulación del teorema de Green.
10.15.2 Aplicar la forma de flujo del teorema de Green.
10.15.3 Calcular la circulación y el flujo en regiones más generales.
En esta sección, examinamos el teorema de Green, que es una extensión del Teorema Fundamental del Cálculo a dos dimensiones. El teorema de Green tiene dos formas: una forma de circulación y una forma de flujo, ambas requieren que la región D en la integral doble sea simplemente conexa. Sin embargo, extenderemos el teorema de Green a regiones que no son simplemente conexas.
En términos simples, el teorema de Green relaciona una integral de línea alrededor de una curva plana cerrada y simplemente conexa C con una integral doble sobre la región encerrada por C. El teorema es útil porque nos permite transformar integrales de línea difíciles en integrales dobles más simples, o integrales dobles difíciles en integrales de línea más simples.
Extendiendo el Teorema Fundamental del Cálculo
Recuerda que el Teorema Fundamental del Cálculo establece que
\[ \displaystyle \int_{a}^{b} F'(x) \, dx = F(b) – F(a). \]Como una afirmación geométrica, esta ecuación dice que la integral sobre la región debajo de la gráfica de \(F'(x)\) y por encima del segmento de línea \([a, b]\) depende únicamente del valor de \(F\) en los puntos extremos \(a\) y \(b\) de ese segmento. Dado que los números \(a\) y \(b\) son el límite del segmento de línea \([a, b]\), el teorema dice que podemos calcular la integral \(\displaystyle \int_{a}^{b} F'(x) \, dx\) basándonos en información sobre el límite del segmento de línea \([a, b]\) (Figura 10.15.1). La misma idea es válida para el Teorema Fundamental para Integrales de Línea:
\[ \displaystyle \int_{C} \nabla f \cdot d\mathbf{r} = f(\mathbf{r}(b)) \, – \, f(\mathbf{r}(a)). \]Cuando tenemos una función potencial (una “antiderivada”), podemos calcular la integral de línea basándonos únicamente en información sobre el límite de la curva \(C\).
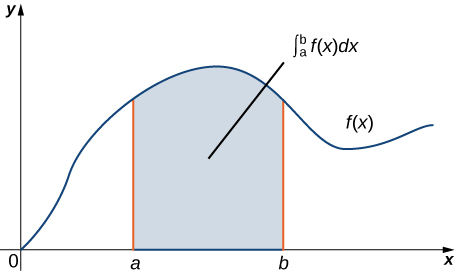
Figura 10.15.1 El Teorema Fundamental del Cálculo establece que la integral sobre el segmento de línea [a, b] depende únicamente de los valores de la antiderivada en los puntos extremos de [a, b].
El teorema de Green toma esta idea y la extiende al cálculo de integrales dobles. El teorema de Green establece que podemos calcular una integral doble sobre una región D basándonos únicamente en la información sobre la frontera de D. Además, el teorema de Green también indica que podemos calcular una integral de línea sobre una curva cerrada simple C basándonos únicamente en la información sobre la región que C encierra. En particular, el teorema de Green conecta una integral doble sobre la región D con una integral de línea alrededor de la frontera de D.
Forma de Circulación del Teorema de Green
La primera forma del teorema de Green que examinamos es la forma de circulación. Esta forma del teorema relaciona la integral de línea vectorial sobre una curva plana simple y cerrada C con una integral doble sobre la región encerrada por C. Por lo tanto, la circulación de un campo vectorial a lo largo de una curva cerrada simple puede transformarse en una integral doble, y viceversa.
Teorema 10.15.1: Teorema de Green, Forma de Circulación
Sea \( D \) una región abierta y simplemente conexa con una curva de frontera \( C \) que es una curva cerrada simple, suave por partes y orientada en sentido antihorario (Figura 10.15.2). Sea \( \mathbf{F} = \langle P, Q \rangle \) un campo vectorial cuyas funciones componentes tienen derivadas parciales continuas en \( D \). Entonces,
\[ \int_C \mathbf{F} \cdot d\mathbf{r} = \int_C P \, dx + Q \, dy = \iint_D (Q_x – P_y) \, dA. \]♦
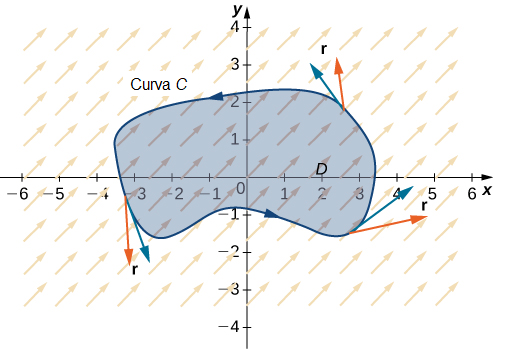
Figura 10.15.2 La forma de circulación del teorema de Green relaciona una integral de línea sobre la curva C con una integral doble sobre la región D.
Observa que el teorema de Green solo puede aplicarse a un campo vectorial bidimensional \( \mathbf{F} \). Si \( \mathbf{F} \) es un campo tridimensional, entonces el teorema de Green no se aplica. Dado que
\[ \int_{C} P \, dx + Q \, dy = \int_{C} \mathbf{F} \cdot \mathbf{T} \, ds, \]esta versión del teorema de Green a veces se conoce como la forma tangencial del teorema de Green.
La demostración del teorema de Green es bastante técnica y está más allá del alcance de este texto. Aquí examinamos una demostración del teorema en el caso especial en que \( D \) es un rectángulo. Por ahora, observa que podemos confirmar rápidamente que el teorema es cierto para el caso especial en el que \( \mathbf{F} = \langle P, Q \rangle \) es conservativo. En este caso,
\[ \int_{C} P \, dx + Q \, dy = 0 \]porque la circulación es cero en campos vectoriales conservativos. Por la Propiedad de las Derivadas Cruzadas para Campos Conservativos, \( \mathbf{F} \) satisface la condición de las derivadas cruzadas, es decir, \( P_y = Q_x \). Por lo tanto,
\[ \iint_{D} (Q_x – P_y) \, dA = \iint_{D} 0 \, dA = 0 = \int_{C} P \, dx + Q \, dy, \]lo que confirma el teorema de Green en el caso de campos vectoriales conservativos.
Prueba:
Ahora demostremos que la forma de circulación del teorema de Green es cierta cuando la región \( D \) es un rectángulo. Sea \( D \) el rectángulo \([a, b] \times [c, d]\) orientado en sentido antihorario. Entonces, el límite \( C \) de \( D \) consta de cuatro partes suaves por tramos: \( C_1, C_2, C_3 \) y \( C_4 \) (Figura 6.34). Parametrizamos cada lado de \( D \) de la siguiente manera:
\[ C_1 : \mathbf{r}_1(t) = \langle t, c \rangle, \quad a \leq t \leq b \] \[ C_2 : \mathbf{r}_2(t) = \langle b, t \rangle, \quad c \leq t \leq d \] \[ -C_3 : \mathbf{r}_3(t) = \langle t, d \rangle, \quad a \leq t \leq b \] \[ -C_4 : \mathbf{r}_4(t) = \langle a, t \rangle, \quad c \leq t \leq d. \]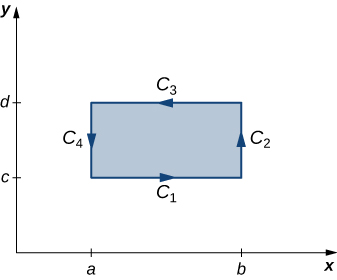
Figura 10.15.3 El rectángulo D está orientado en sentido antihorario.
Entonces,
\[ \int_C \mathbf{F} \cdot d\mathbf{r} = \int_{C_1} \mathbf{F} \cdot d\mathbf{r} + \int_{C_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C_3} \mathbf{F} \cdot d\mathbf{r} + \int_{C_4} \mathbf{F} \cdot d\mathbf{r} \] \[ = \int_{C_1} \mathbf{F} \cdot d\mathbf{r} + \int_{C_2} \mathbf{F} \cdot d\mathbf{r} – \int_{-C_3} \mathbf{F} \cdot d\mathbf{r} – \int_{-C_4} \mathbf{F} \cdot d\mathbf{r} \] \[ = \int_a^b \mathbf{F} (\mathbf{r}_1(t)) \cdot \mathbf{r}_1′(t) \, dt + \int_c^d \mathbf{F} (\mathbf{r}_2(t)) \cdot \mathbf{r}_2′(t) \, dt \] \[ – \int_a^b \mathbf{F} (\mathbf{r}_3(t)) \cdot \mathbf{r}_3′(t) \, dt – \int_c^d \mathbf{F} (\mathbf{r}_4(t)) \cdot \mathbf{r}_4′(t) \, dt \] \[ = \int_a^b P(t, c) \, dt + \int_c^d Q(b, t) \, dt – \int_a^b P(t, d) \, dt – \int_c^d Q(a, t) \, dt \] \[ = \int_a^b \left( P(t, c) – P(t, d) \right) dt + \int_c^d \left( Q(b, t) – Q(a, t) \right) dt \] \[ = – \int_a^b \left( P(t, d) – P(t, c) \right) dt + \int_c^d \left( Q(b, t) – Q(a, t) \right) dt. \]Por el Teorema Fundamental del Cálculo,
\[ P(t, d) – P(t, c) = \int_c^d \frac{\partial}{\partial y} P(t, y) \, dy \quad \text{y} \quad Q(b, t) – Q(a, t) = \int_a^b \frac{\partial}{\partial x} Q(x, t) \, dx. \]Por lo tanto,
\[ – \int_a^b \left( P(t, d) – P(t, c) \right) dt + \int_c^d \left( Q(b, t) – Q(a, t) \right) dt \] \[ = – \int_a^b \int_c^d \frac{\partial}{\partial y} P(t, y) \, dy \, dt + \int_c^d \int_a^b \frac{\partial}{\partial x} Q(x, t) \, dx \, dt. \]Pero,
\[ – \int_a^b \int_c^d \frac{\partial}{\partial y} P(t, y) \, dy \, dt + \int_c^d \int_a^b \frac{\partial}{\partial x} Q(x, t) \, dx \, dt = – \int_a^b \int_c^d \frac{\partial}{\partial y} P(x, y) \, dy \, dx + \int_c^d \int_a^b \frac{\partial}{\partial x} Q(x, y) \, dx \, dy \] \[ = \int_a^b \int_c^d \left( Q_x – P_y \right) dy \, dx \] \[ = \int_D \left( Q_x – P_y \right) dA. \]Por lo tanto,
\[ \int_C \mathbf{F} \cdot d\mathbf{r} = \int_D \left( Q_x – P_y \right) dA, \]y hemos demostrado el teorema de Green en el caso de un rectángulo.
Para demostrar el teorema de Green sobre una región general \( D \), podemos descomponer \( D \) en muchos rectángulos pequeños y usar la demostración de que el teorema funciona sobre rectángulos. Sin embargo, los detalles son técnicos y están más allá del alcance de este texto. ♦
Ejemplo ilustrativo 10.15.1: Aplicando el Teorema de Green sobre un Rectángulo
Calcula la integral de línea
\[ \int_{C} x^2 y \, dx + (y – 3) \, dy, \]donde \( C \) es un rectángulo con vértices \( (1, 1) \), \( (4, 1) \), \( (4, 5) \) y \( (1, 5) \), orientado en sentido antihorario.
Solución:
Sea \( \mathbf{F}(x, y) = \langle P(x, y), Q(x, y) \rangle = \langle x^2y, y – 3 \rangle \). Entonces, \( Q_x = 0 \) y \( P_y = x^2 \). Por lo tanto, \( Q_x – P_y = -x^2 \).
Sea \( D \) la región rectangular encerrada por \( C \) (Figura 10.15.4). Por el teorema de Green,
\[ \int_C x^2y \, dx + (y – 3) \, dy = \iint_D (Q_x – P_y) \, dA \] \[ = \int_1^5 \int_1^4 -x^2 \, dx \, dy \] \[ = \int_1^5 -21 \, dy = -84. \]
Figura 10.15.4 La integral de línea sobre la frontera del rectángulo puede transformarse en una integral doble sobre el rectángulo.
Análisis:
Si quisiéramos evaluar esta integral de línea sin usar el teorema de Green, tendríamos que parametrizar cada lado del rectángulo, dividir la integral de línea en cuatro integrales de línea separadas y usar los métodos de Integrales de Línea para evaluar cada integral. Además, dado que el campo vectorial aquí no es conservativo, no podemos aplicar el Teorema Fundamental de las Integrales de Línea. El teorema de Green simplifica enormemente el cálculo. ♦
Ejemplo ilustrativo 10.15.2: Aplicando el Teorema de Green para Calcular Trabajo
Calcula el trabajo realizado sobre una partícula por el campo de fuerza
\[ \mathbf{F}(x, y) = \langle y + \sin x, e^y – x \rangle \]mientras la partícula recorre el círculo \( x^2 + y^2 = 4 \) exactamente una vez en dirección antihoraria, comenzando y terminando en el punto \((2, 0)\).
Solución:
Sea \( C \) el círculo y \( D \) el disco encerrado por \( C \). El trabajo realizado sobre la partícula es
\[ W = \int_{C} (y + \sin x) \, dx + (e^y – x) \, dy. \]Al igual que en el Ejemplo anterior, esta integral se puede calcular utilizando las herramientas que hemos aprendido, pero es más fácil usar la integral doble dada por el teorema de Green (Figura 10.15.5).
Sea \( \mathbf{F}(x, y) = \langle P(x, y), Q(x, y) \rangle = \langle y + \sin x, e^y – x \rangle \). Entonces, \( Q_x = -1 \) y \( P_y = 1 \). Por lo tanto, \( Q_x – P_y = -2 \).
Por el teorema de Green,
\[ W = \int_{C} (y + \sin(x)) \, dx + (e^y – x) \, dy \] \[ = \iint_{D} (Q_x – P_y) \, dA = \iint_{D} -2 \, dA \] \[ = -2 \cdot \text{área}(D) = -2 \pi (2^2) = -8 \pi. \]
Figura 10.15.5 La integral de línea sobre la frontera del círculo puede transformarse en una integral doble sobre el disco encerrado por el círculo. ♦
Ejercicio de control 10.15.1
Usa el teorema de Green para calcular la integral de línea
\[ \int_{C} \sin(x^2) \, dx + (3x – y) \, dy, \]donde \( C \) es un triángulo rectángulo con vértices \((-1, 2)\), \((4, 2)\) y \((4, 5)\), orientado en sentido antihorario. ♦
En los dos ejemplos anteriores, la integral doble en el teorema de Green fue más fácil de calcular que la integral de línea, por lo que utilizamos el teorema para calcular la integral de línea. En el siguiente ejemplo, la integral doble es más difícil de calcular que la integral de línea, por lo que usamos el teorema de Green para transformar una integral doble en una integral de línea.
Ejemplo ilustrativo 10.15.3: Aplicando el Teorema de Green sobre una Elipse
Calcula el área encerrada por la elipse \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) (Figura 10.15.6).
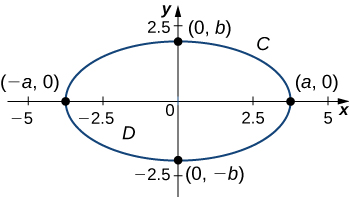
Figura 10.15.6: La elipse \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) se denota por \( C \).
Solución:
Sea \( C \) la elipse y \( D \) la región encerrada por \( C \). Recuerda que la elipse \( C \) puede parametrizarse como
\[ x = a \cos t, \quad y = b \sin t, \quad 0 \leq t \leq 2\pi. \]Calcular el área de \( D \) es equivalente a calcular la integral doble \(\iint_D dA\). Para calcular esta integral sin el teorema de Green, necesitaríamos dividir \( D \) en dos regiones: la región por encima del eje \( x \) y la región por debajo. El área de la elipse es
\[ \int_{-a}^{a} \int_{0}^{\sqrt{b^2-(bx/a)^2}} dy \, dx + \int_{-a}^{a} \int_{-\sqrt{b^2-(bx/a)^2}}^{0} dy \, dx. \]Estas dos integrales no son sencillas de calcular (aunque, si conocemos el valor de la primera integral, por simetría conocemos el valor de la segunda). En lugar de intentar calcularlas, usamos el teorema de Green para transformar \(\iint_D dA\) en una integral de línea alrededor del límite \( C \).
Considera el campo vectorial
\[ \mathbf{F}(x, y) = \langle P, Q \rangle = \left\langle -\frac{y}{2}, \frac{x}{2} \right\rangle. \]Entonces, \( Q_x = \frac{1}{2} \) y \( P_y = -\frac{1}{2} \), y por lo tanto \( Q_x – P_y = 1 \). Observa que \( \mathbf{F} \) se eligió para tener la propiedad de que \( Q_x – P_y = 1 \). Dado que este es el caso, el teorema de Green transforma la integral de línea de \( \mathbf{F} \) sobre \( C \) en la integral doble de 1 sobre \( D \).
Por el teorema de Green,
\[ \begin{aligned} \iint_D dA &= \iint_D (Q_x – P_y) \, dA \\ &= \int_C \mathbf{F} \cdot d\mathbf{r} \\ &= \frac{1}{2} \int_C -y \, dx + x \, dy \\ &= \frac{1}{2} \int_0^{2\pi} -b \sin t (-a \sin t) + a (\cos t) b \cos t \, dt \\ &= \frac{1}{2} \int_0^{2\pi} ab \cos^2 t + ab \sin^2 t \, dt \\ &= \frac{1}{2} \int_0^{2\pi} ab \, dt \\ &= \pi ab. \end{aligned} \]Por lo tanto, el área de la elipse es \(\pi ab\). ♦
En el Ejemplo anterior, usamos el campo vectorial \( \mathbf{F}(x, y) = \langle P, Q \rangle = \left\langle -\frac{y}{2}, \frac{x}{2} \right\rangle \) para encontrar el área de cualquier elipse. La lógica del ejemplo anterior se puede extender para derivar una fórmula para el área de cualquier región \( D \). Sea \( D \) cualquier región con un límite que es una curva cerrada simple \( C \) orientada en sentido antihorario. Si \( \mathbf{F}(x, y) = \langle P, Q \rangle = \left\langle -\frac{y}{2}, \frac{x}{2} \right\rangle \), entonces \( Q_x – P_y = 1 \). Por lo tanto, siguiendo la misma lógica que en el Ejemplo anterior,
\[ \text{área de } D = \iint_D dA = \frac{1}{2} \int_C -y \, dx + x \, dy. (10.15.1) \]Vale la pena señalar que si \( \mathbf{F} = \langle P, Q \rangle \) es cualquier campo vectorial con \( Q_x – P_y = 1 \), entonces la lógica del párrafo anterior funciona. Por lo tanto, la Ecuación 10.15.1 no es la única ecuación que utiliza las derivadas parciales mixtas de un campo vectorial para obtener el área de una región.
Ejercicio de control 10.15.2
Encuentra el área de la región encerrada por la curva con parametrización
\[ \mathbf{r}(t) = \langle \sin t \cos t, \sin t \rangle, \quad 0 \leq t \leq \pi. \]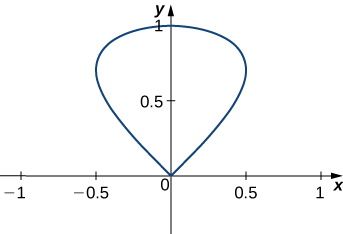
♦
Forma de Flujo del Teorema de Green
La forma de circulación del teorema de Green relaciona una integral doble sobre la región \( D \) con una integral de línea \(\int_C \mathbf{F} \cdot \mathbf{T} \, ds\), donde \( C \) es el límite de \( D \). La forma de flujo del teorema de Green relaciona una integral doble sobre la región \( D \) con el flujo a través del límite \( C \). El flujo de un fluido a través de una curva puede ser difícil de calcular utilizando la integral de línea de flujo. Esta forma del teorema de Green nos permite traducir una integral de flujo complicada en una integral doble que a menudo es más fácil de calcular.
Teorema 10.15.2: Teorema de Green, Forma de Flujo
Sea \( D \) una región abierta y simplemente conexa con una curva de frontera \( C \) que es una curva cerrada simple, suave por partes y orientada en sentido antihorario (Figura 10.15.7). Sea \( \mathbf{F} = \langle P, Q \rangle \) un campo vectorial cuyas funciones componentes tienen derivadas parciales continuas en una región abierta que contiene \( D \). Entonces,
\[ \int_C \mathbf{F} \cdot \mathbf{N} \, ds = \iint_D (P_x + Q_y) \, dA. (10.15.2) \]♦

Figura 10.15.7 La forma de flujo del teorema de Green relaciona una integral doble sobre la región D con el flujo a través de la curva C.
Debido a que esta forma del teorema de Green incluye el vector normal unitario N, a veces se la conoce como la forma normal del teorema de Green.
Prueba:
Recuerda que
\[ \int_C \mathbf{F} \cdot \mathbf{N} \, ds = \int_C -Q \, dx + P \, dy. \]Sea \( M = -Q \) y \( N = P \). Por la forma de circulación del teorema de Green,
\[ \begin{aligned} \int_C -Q \, dx + P \, dy &= \int_C M \, dx + N \, dy \\ &= \iint_D (N_x – M_y) \, dA \\ &= \iint_D (P_x – (-Q)_y) \, dA \\ &= \iint_D (P_x + Q_y) \, dA. \end{aligned} \]♦
Ejemplo ilustrativo 10.15.4: Aplicando el Teorema de Green para el Flujo a través de un Círculo
Sea \( C \) un círculo de radio \( r \) centrado en el origen (Figura 10.15.8) y sea \( \mathbf{F}(x, y) = \langle x, y \rangle \). Calcula el flujo a través de \( C \).
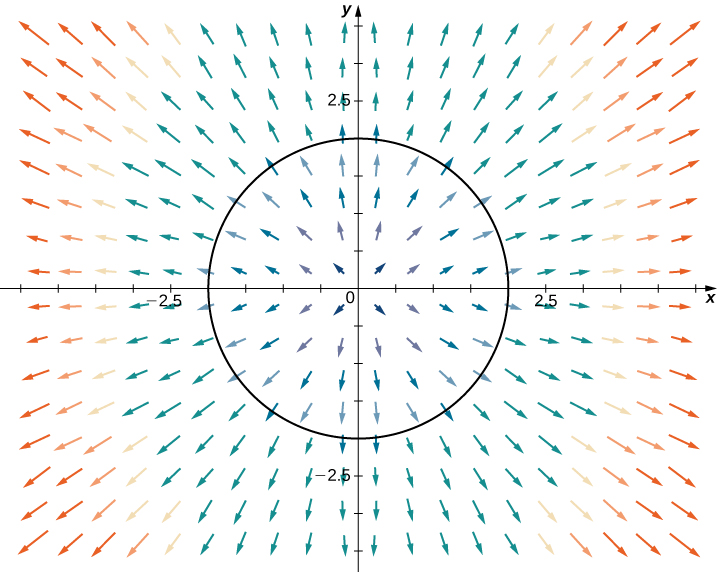
Figura 10.15.8 La curva C es un círculo de radio r centrado en el origen.
Solución:
Sea \( D \) el disco encerrado por \( C \). El flujo a través de \( C \) es
\[ \int_C \mathbf{F} \cdot \mathbf{N} \, ds. \]Podríamos evaluar esta integral utilizando las herramientas que hemos aprendido, pero el teorema de Green simplifica mucho el cálculo. Sea \( P(x, y) = x \) y \( Q(x, y) = y \), de modo que \( \mathbf{F} = \langle P, Q \rangle \). Observa que \( P_x = 1 = Q_y \), y por lo tanto \( P_x + Q_y = 2 \). Por el teorema de Green,
\[ \int_C \mathbf{F} \cdot \mathbf{N} \, ds = \iint_D 2 \, dA = 2 \iint_D dA. \]Dado que \(\iint_D dA\) es el área del círculo,
\[ \iint_D dA = \pi r^2. \]Por lo tanto, el flujo a través de \( C \) es \( 2\pi r^2 \). ♦
Ejemplo ilustrativo 10.15.5: Aplicando el Teorema de Green para el Flujo a través de un Triángulo
Sea \( S \) el triángulo con vértices \( (0, 0) \), \( (1, 0) \) y \( (0, 3) \) orientado en sentido horario (Figura 10.15.9). Calcula el flujo de \( \mathbf{F}(x, y) = \langle P(x, y), Q(x, y) \rangle = \langle x^2 + e^y, x + y \rangle \) a través de \( S \).

Figura 10.15.9 La curva S es un triángulo con vértices en (0, 0), (1, 0) y (0, 3), orientado en sentido horario.
Solución:
Para calcular el flujo sin el teorema de Green, necesitaríamos dividir la integral de flujo en tres integrales de línea, una integral para cada lado del triángulo. Usar el teorema de Green para traducir la integral de línea de flujo en una única integral doble es mucho más sencillo.
Sea \( D \) la región encerrada por \( S \). Observa que \( P_x = 2x \) y \( Q_y = 1 \); por lo tanto, \( P_x + Q_y = 2x + 1 \).
El teorema de Green se aplica solo a curvas cerradas simples orientadas en sentido antihorario, pero aún podemos aplicar el teorema porque
\[ \int_C \mathbf{F} \cdot \mathbf{N} \, ds = – \int_{-S} \mathbf{F} \cdot \mathbf{N} \, ds \]y \(-S\) está orientada en sentido antihorario.
Por el teorema de Green, el flujo es
\[ \begin{aligned} \int_C \mathbf{F} \cdot \mathbf{N} \, ds &= \int_{-S} \mathbf{F} \cdot \mathbf{N} \, ds \\ &= – \iint_D (P_x + Q_y) \, dA \\ &= – \iint_D (2x + 1) \, dA. \end{aligned} \]Observa que el borde superior del triángulo es la línea \( y = -3x + 3 \). Por lo tanto, en la integral doble iterada, los valores de \( y \) van desde \( y = 0 \) hasta \( y = -3x + 3 \), y tenemos
\[ \begin{aligned} – \iint_D (2x + 1) \, dA &= – \int_0^1 \int_0^{-3x+3} (2x + 1) \, dy \, dx \\ &= – \int_0^1 (2x + 1)(-3x + 3) \, dx \\ &= – \int_0^1 (-6x^2 + 3x + 3) \, dx \\ &= – \left[ -2x^3 + \frac{3x^2}{2} + 3x \right]_0^1 \\ &= -\frac{5}{2}. \end{aligned} \]♦
Ejercicio de control 10.15.3
Calcula el flujo de \( \mathbf{F}(x, y) = \langle x^3, y^3 \rangle \) a través de un círculo unitario orientado en sentido antihorario. ♦
Ejemplo ilustrativo 10.15.6: Aplicando el Teorema de Green para el Flujo de Agua a través de un Rectángulo
El agua fluye desde un manantial ubicado en el origen. La velocidad del agua se modela mediante el campo vectorial
\[ \mathbf{v}(x, y) = (5x + y, x + 3y) \, \text{m/sec}. \]Encuentra la cantidad de agua por segundo que fluye a través del rectángulo con vértices \((-1, -2)\), \((1, -2)\), \((1, 3)\) y \((-1, 3)\), orientado en sentido antihorario (Figura 10.15.10).

Figura 10.15.10 El agua fluye a través del rectángulo con vértices en (−1, −2), (1, −2), (1, 3) y (−1, 3), orientado en sentido antihorario.
Solución:
Sea \( C \) el rectángulo dado y \( D \) la región rectangular encerrada por \( C \). Para encontrar la cantidad de agua que fluye a través de \( C \), calculamos el flujo
\[ \int_C \mathbf{v} \cdot \mathbf{N} \, \mathrm{d}\mathbf{s}. \]Sea \( P(x, y) = 5x + y \) y \( Q(x, y) = x + 3y \), de modo que \( \mathbf{v} = (P, Q) \). Entonces, \( P_x = 5 \) y \( Q_y = 3 \). Por el teorema de Green,
\[ \begin{aligned} \int_C \mathbf{v} \cdot \mathbf{N} \, \mathrm{d}\mathbf{s} &= \iint_D (P_x + Q_y) \, dA \\ &= \iint_D 8 \, dA \\ &= 8 \, (\text{área de } D) \\ &= 80. \end{aligned} \]Por lo tanto, el flujo de agua es \( 80 \, \text{m}^2/\text{seg} \). ♦
Recuerda que si un campo vectorial \( \mathbf{F} \) es conservativo, entonces \( \mathbf{F} \) no realiza trabajo alrededor de curvas cerradas, es decir, la circulación de \( \mathbf{F} \) alrededor de una curva cerrada es cero. De hecho, si el dominio de \( \mathbf{F} \) es simplemente conexo, entonces \( \mathbf{F} \) es conservativo si y solo si la circulación de \( \mathbf{F} \) alrededor de cualquier curva cerrada es cero. Si reemplazamos “circulación de \( \mathbf{F} \)” con “flujo de \( \mathbf{F} \)”, obtenemos una definición de un campo vectorial libre de fuentes. Las siguientes afirmaciones son formas equivalentes de definir un campo libre de fuentes \( \mathbf{F} = \langle P, Q \rangle \) en un dominio simplemente conexo (observa las similitudes con las propiedades de los campos vectoriales conservativos):
- El flujo \[ \int_C \mathbf{F} \cdot \mathbf{N} \, ds \] a través de cualquier curva cerrada \( C \) es cero.
- Si \( C_1 \) y \( C_2 \) son curvas en el dominio de \( \mathbf{F} \) con los mismos puntos iniciales y finales, entonces
En otras palabras, el flujo es independiente de la trayectoria.
- Existe una función de corriente \( g(x, y) \) para \( \mathbf{F} \). Una función de corriente para \( \mathbf{F} = \langle P, Q \rangle \) es una función \( g \) tal que \( P = g_y \) y \( Q = -g_x \). Geométricamente, \( \mathbf{F}(a, b) \) es tangente a la curva de nivel de \( g \) en \( (a, b) \). Dado que el gradiente de \( g \) es perpendicular a la curva de nivel de \( g \) en \( (a, b) \), la función de corriente \( g \) tiene la propiedad \( \mathbf{F}(a, b) \cdot \nabla g(a, b) = 0 \) para cualquier punto \( (a, b) \) en el dominio de \( g \). (Las funciones de corriente juegan el mismo papel para los campos libres de fuentes que las funciones potenciales juegan para los campos conservativos).
- \[ P_x + Q_y = 0 \]
Ejemplo ilustrativo 10.15.7: Encontrando una Función de Corriente
Verificar que el campo vectorial de rotación \(\mathbf{F}(x, y) = \langle y, -x \rangle\) es libre de fuentes, y encontrar una función de corriente para \(\mathbf{F}\).Solución:
Observa que el dominio de \( F \) es todo \(\mathbb{R}^2\), que es simplemente conexo. Por lo tanto, para mostrar que \( F \) es libre de fuentes, podemos mostrar que cualquiera de los elementos 1 al 4 de la lista anterior es verdadero. En este ejemplo, mostramos que el elemento 4 es verdadero. Sean \( P(x,y) = y \) y \( Q(x,y) = -x \). Entonces \( P_x + 0 = Q_y \), y por lo tanto \( P_x + Q_y = 0 \). Así, \( F \) es libre de fuentes. Para encontrar una función de corriente para \( F \), procedemos de la misma manera que para encontrar una función potencial para un campo conservativo. Sea \( g \) una función de corriente para \( F \). Entonces \( g_y = y \), lo que implica que \[g(x,y) = \frac{y^2}{2} + h(x).\] Dado que \(-g_x = Q = -x\), tenemos \( h'(x) = x \). Por lo tanto, \[h(x) = \frac{x^2}{2} + C.\] Tomando \( C = 0 \), obtenemos la función de corriente \[g(x,y) = \frac{x^2}{2} + \frac{y^2}{2}.\] Para confirmar que \( g \) es una función de corriente para \( F \), observa que \( g_y = y = P \) y \(-g_x = -x = Q \). Observa que el campo vectorial de rotación libre de fuentes \( F(x,y) = \langle y, -x \rangle \) es perpendicular al campo vectorial radial conservativo \( \nabla g = \langle x, y \rangle \) (Figura 10.15.11).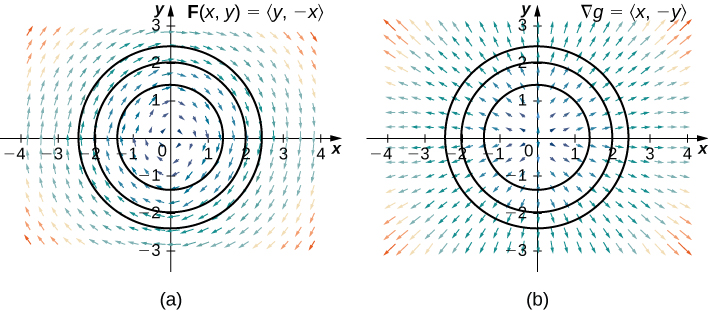
Figura 10.15.11 (a) En esta imagen, vemos las tres curvas de nivel de \( g \) y el campo vectorial \( \mathbf{F} \). Observa que los vectores de \( \mathbf{F} \) en una curva de nivel dada son tangentes a la curva de nivel. (b) En esta imagen, vemos las tres curvas de nivel de \( g \) y el campo vectorial \( \nabla g \). Los vectores gradientes son perpendiculares a la curva de nivel correspondiente. Por lo tanto, \( \mathbf{F}(a, b) \cdot \nabla g(a, b) = 0 \) para cualquier punto en el dominio de \( g \). ♦
Ejercicio de control 10.15.4
Encuentra una función de corriente para el campo vectorial \(\mathbf{F}\left(x, y\right) = \left\langle x \sin y, \cos y \right\rangle\). ♦
Los campos vectoriales que son tanto conservativos como libres de fuentes son campos vectoriales importantes. Una característica importante de los campos vectoriales conservativos y libres de fuentes en un dominio simplemente conexo es que cualquier función potencial \( f \) de dicho campo satisface la ecuación de Laplace \( f_{xx} + f_{yy} = 0 \). La ecuación de Laplace es fundamental en el campo de las ecuaciones diferenciales parciales porque modela fenómenos como los potenciales gravitacionales y magnéticos en el espacio, y el potencial de velocidad de un fluido ideal. Una función que satisface la ecuación de Laplace se llama función armónica. Por lo tanto, cualquier función potencial de un campo vectorial conservativo y libre de fuentes es armónica.
Para ver que cualquier función potencial de un campo vectorial conservativo y libre de fuentes en un dominio simplemente conexo es armónica, sea \( f \) tal función potencial del campo vectorial \( \mathbf{F} = \langle P, Q \rangle \). Entonces, \( f_x = P \) y \( f_y = Q \) porque \( \nabla f = \mathbf{F} \). Por lo tanto, \( f_{xx} = P_x \) y \( f_{yy} = Q_y \). Dado que \( \mathbf{F} \) es libre de fuentes, \( f_{xx} + f_{yy} = P_x + Q_y = 0 \), y tenemos que \( f \) es armónica.
Ejemplo ilustrativo 10.15.8: Satisfaciendo la Ecuación de Laplace
Para el campo vectorial \(\mathbf{F}\left(x, y\right) = \langle e^{x} \sin y, e^{x} \cos y \rangle\), verifica que el campo es tanto conservativo como libre de fuentes, encuentra una función potencial para \(\mathbf{F}\), y verifica que la función potencial es armónica.
Solución:
Sea \( P(x, y) = e^x \sin y \) y \( Q(x, y) = e^x \cos y \). Observa que el dominio de \(\mathbf{F}\) es todo el espacio bidimensional, que es simplemente conexo. Por lo tanto, podemos verificar las derivadas parciales cruzadas de \(\mathbf{F}\) para determinar si \(\mathbf{F}\) es conservativo. Nota que \( P_y = e^x \cos y = Q_x \), por lo que \(\mathbf{F}\) es conservativo. Como \( P_x = e^x \sin y \) y \( Q_y = -e^x \sin y \), se cumple que \( P_x + Q_y = 0 \) y el campo es libre de fuentes.
Para encontrar una función potencial para \(\mathbf{F}\), sea \( f \) una función potencial. Entonces, \( \nabla f = \mathbf{F} \), por lo que \( f_x = e^x \sin y \). Integrando esta ecuación con respecto a \( x \) se obtiene \( f(x, y) = e^x \sin y + h(y) \). Como \( f_y = e^x \cos y \), diferenciando \( f \) con respecto a \( y \) se obtiene \( e^x \cos y = e^x \cos y + h'(y) \). Por lo tanto, podemos tomar \( h(y) = 0 \), y \( f(x, y) = e^x \sin y \) es una función potencial para \( f \).
Para verificar que \( f \) es una función armónica, observa que \( f_{xx} = \frac{\partial}{\partial x} (e^x \sin y) = e^x \sin y \) y \[ f_{yy} = \frac{\partial}{\partial y} (e^x \cos y) = -e^x \sin y. \] Por lo tanto, \( f_{xx} + f_{yy} = 0 \), y \( f \) satisface la ecuación de Laplace. ♦
Ejercicio de control 10.15.5
¿Es la función \( f\left(x, y\right) = e^{x + 5y} \) armónica? ♦
Teorema de Green en Regiones Generales
El teorema de Green, tal como se ha enunciado, se aplica solo a regiones que son simplemente conexas, es decir, el teorema de Green, tal como se ha expuesto hasta ahora, no puede manejar regiones con agujeros. Aquí, extendemos el teorema de Green para que funcione en regiones con un número finito de agujeros (Figura 10.15.12).

Figura 10.15.12 El teorema de Green, tal como se ha enunciado, no se aplica a una región no simplemente conexa con tres agujeros como esta.
Antes de discutir las extensiones del teorema de Green, necesitamos repasar alguna terminología relacionada con la frontera de una región. Sea D una región y sea C una componente de la frontera de D. Decimos que C está orientada positivamente si, mientras caminamos a lo largo de C en la dirección de orientación, la región D está siempre a nuestra izquierda. Por lo tanto, la orientación antihoraria de la frontera de un disco es una orientación positiva, por ejemplo. La curva C está orientada negativamente si, mientras caminamos a lo largo de C en la dirección de orientación, la región D está siempre a nuestra derecha. La orientación horaria de la frontera de un disco es una orientación negativa, por ejemplo.
Sea \( D \) una región con un número finito de agujeros (de modo que \( D \) tiene un número finito de curvas de frontera), y denotemos la frontera de \( D \) por \( \partial D \) (Figura 10.15.13). Para extender el teorema de Green de manera que pueda manejar \( D \), dividimos la región \( D \) en dos regiones, \( D_1 \) y \( D_2 \) (con fronteras respectivas \( \partial D_1 \) y \( \partial D_2 \)), de tal manera que \( D = D_1 \cup D_2 \) y ni \( D_1 \) ni \( D_2 \) tengan agujeros (Figura 10.15.13).
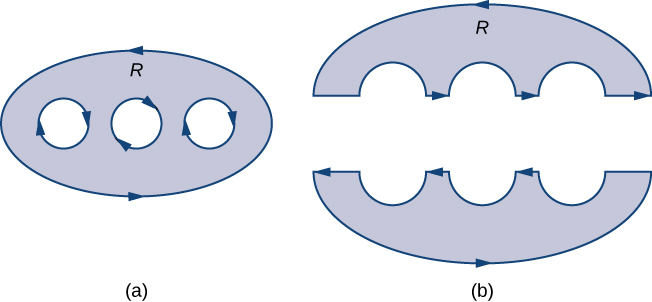
Figura 10.15.13 (a) La región D con una frontera orientada tiene tres agujeros. (b) La región D dividida en dos regiones simplemente conexas no tiene agujeros.
Supongamos que la frontera de \( D \) está orientada como en la figura, con los agujeros internos con una orientación negativa y la frontera exterior con una orientación positiva. La frontera de cada región simplemente conexa \( \mathbf{D}_1 \) y \( \mathbf{D}_2 \) está orientada positivamente. Si \( \mathbf{F} \) es un campo vectorial definido en \( D \), entonces el teorema de Green dice que
\[ \int_{\partial D} \mathbf{F} \cdot d\mathbf{r} = \int_{\partial D_1} \mathbf{F} \cdot d\mathbf{r} + \int_{\partial D_2} \mathbf{F} \cdot d\mathbf{r} \] \[ = \iint_{D_1} Q_x – P_y \, dA + \iint_{D_2} Q_x – P_y \, dA \] \[ = \iint_D (Q_x – P_y) \, dA. \]Por lo tanto, el teorema de Green sigue funcionando en una región con agujeros.
Para ver cómo funciona esto en la práctica, considera el anillo \( D \) en la Figura 10.15.14 y supongamos que \( \mathbf{F} = \langle P, Q \rangle \) es un campo vectorial definido en este anillo. La región \( D \) tiene un agujero, por lo que no es simplemente conexa. Orienta el círculo exterior del anillo en sentido contrario a las manecillas del reloj y el círculo interior en sentido horario (Figura 10.15.14) de modo que, al dividir la región en \( \mathbf{D}_1 \) y \( \mathbf{D}_2 \), podamos mantener la región a nuestra izquierda mientras recorremos un camino que atraviesa la frontera. Sea \( \mathbf{D}_1 \) la mitad superior del anillo y \( \mathbf{D}_2 \) la mitad inferior. Ninguna de estas regiones tiene agujeros, por lo que hemos dividido \( D \) en dos regiones simplemente conexas.
Etiquetamos cada pieza de estas nuevas fronteras como \( P_i \) para algún \( i \), como en la Figura 10.15.14. Si comenzamos en \( P \) y viajamos a lo largo de la frontera orientada, el primer segmento es \( \mathbf{P}_1 \), luego \( \mathbf{P}_2 \), \( \mathbf{P}_3 \), y \( \mathbf{P}_4 \). Ahora hemos recorrido \( \mathbf{D}_1 \) y regresado a \( P \). A continuación, comenzamos en \( P \) nuevamente y recorremos \( \mathbf{D}_2 \). Dado que la primera pieza de la frontera es la misma que \( \mathbf{P}_4 \) en \( \mathbf{D}_1 \), pero orientada en la dirección opuesta, la primera pieza de \( \mathbf{D}_2 \) es \( -\mathbf{P}_4 \). Luego, tenemos \( \mathbf{P}_5 \), luego \( -\mathbf{P}_2 \), y finalmente \( \mathbf{P}_6 \).
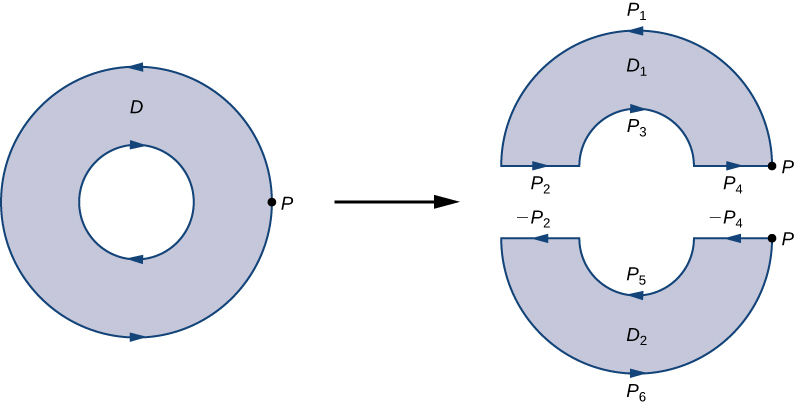
Figura 10.15.14 Dividir el anillo en dos regiones separadas nos da dos regiones simplemente conexas. Las integrales de línea sobre las fronteras comunes se cancelan.
La Figura 10.15.14 muestra un camino que recorre la frontera de \( D \). Observa que este camino recorre la frontera de la región \( D_1 \), regresa al punto de partida y luego recorre la frontera de la región \( D_2 \). Además, mientras caminamos a lo largo del camino, la región siempre está a nuestra izquierda. Observa que este recorrido de los caminos \( P_i \) cubre toda la frontera de la región \( D \). Si solo hubiéramos recorrido una parte de la frontera de \( D \), entonces no podríamos aplicar el teorema de Green a \( D \).
La frontera de la mitad superior del anillo es, por lo tanto, \( P_1 \cup P_2 \cup P_3 \cup P_4 \), y la frontera de la mitad inferior del anillo es \(-P_4 \cup P_5 \cup -P_2 \cup P_6\). Entonces, el teorema de Green implica
\[ \int_{\partial D} \mathbf{F} \cdot d\mathbf{r} = \int_{P_1} \mathbf{F} \cdot d\mathbf{r} + \int_{P_2} \mathbf{F} \cdot d\mathbf{r} + \int_{P_3} \mathbf{F} \cdot d\mathbf{r} + \int_{P_4} \mathbf{F} \cdot d\mathbf{r} + \int_{-P_4} \mathbf{F} \cdot d\mathbf{r} + \int_{P_5} \mathbf{F} \cdot d\mathbf{r} – \int_{P_2} \mathbf{F} \cdot d\mathbf{r} + \int_{P_6} \mathbf{F} \cdot d\mathbf{r} \] \[ = \int_{P_1} \mathbf{F} \cdot d\mathbf{r} + \int_{P_2} \mathbf{F} \cdot d\mathbf{r} + \int_{P_3} \mathbf{F} \cdot d\mathbf{r} + \int_{P_4} \mathbf{F} \cdot d\mathbf{r} – \int_{P_4} \mathbf{F} \cdot d\mathbf{r} + \int_{P_5} \mathbf{F} \cdot d\mathbf{r} – \int_{P_2} \mathbf{F} \cdot d\mathbf{r} + \int_{P_6} \mathbf{F} \cdot d\mathbf{r} \] \[ = \int_{P_1} \mathbf{F} \cdot d\mathbf{r} + \int_{P_3} \mathbf{F} \cdot d\mathbf{r} + \int_{P_5} \mathbf{F} \cdot d\mathbf{r} + \int_{P_6} \mathbf{F} \cdot d\mathbf{r} \] \[ = \int_{\partial D_1} \mathbf{F} \cdot d\mathbf{r} + \int_{\partial D_2} \mathbf{F} \cdot d\mathbf{r} \] \[ = \iint_{D_1} (Q_x – P_y) \, dA + \iint_{D_2} (Q_x – P_y) \, dA \] \[ = \iint_D (Q_x – P_y) \, dA. \]Por lo tanto, llegamos a la ecuación encontrada en el teorema de Green, es decir,
\[ \oint_{\partial D} \mathbf{F} \cdot d\mathbf{r} = \iint_D (Q_x – P_y) \, dA. \]La misma lógica implica que la forma de flujo del teorema de Green también puede extenderse a una región con un número finito de agujeros:
\[ \oint_C \mathbf{F} \cdot \mathbf{N} \, ds = \iint_D (P_x + Q_y) \, dA. \]Ejemplo ilustrativo 10.15.9: Usando el Teorema de Green en una Región con Agujeros
Calcula la integral
\[ \oint_{\partial D} \left( \sin x – \frac{y^3}{3} \right) dx + \left( \frac{x^3}{3} + \sin y \right) dy, \]donde \( D \) es el anillo dado por las desigualdades polares \( 1 \leq r \leq 2, \, 0 \leq \theta \leq 2\pi \).
Solución:
Aunque \( D \) no es simplemente conexa, podemos usar la forma extendida del teorema de Green para calcular la integral. Dado que la integración ocurre sobre un anillo, convertimos a coordenadas polares:
\[ \begin{aligned} \int_{\partial D} \left( \sin x – \frac{y^3}{3} \right) dx + \left( \frac{x^3}{3} + \sin y \right) dy &= \iint_{D} (Q_x – P_y) \, dA \\ &= \iint_{D} (x^2 + y^2) \, dA \\ &= \int_{0}^{2\pi} \int_{1}^{2} r^3 \, dr \, d\theta \\ &= \int_{0}^{2\pi} \frac{15}{4} \, d\theta \\ &= \frac{15\pi}{2}. \end{aligned} \]♦
Ejemplo ilustrativo 10.15.10: Usando la Forma Extendida del Teorema de Green.
Sea \(\mathbf{F} = \langle P, Q \rangle = \left\langle \frac{y}{x^2 + y^2}, -\frac{x}{x^2 + y^2} \right\rangle\) y sea \(C\) cualquier curva cerrada simple en un plano orientada en sentido contrario a las manecillas del reloj. ¿Cuáles son los posibles valores de \(\int_C \mathbf{F} \cdot d\mathbf{r}\)?
Solución:
Usamos la forma extendida del teorema de Green para mostrar que \(\int_C \mathbf{F} \cdot d\mathbf{r}\) es \(0\) o \(-2\pi\); es decir, no importa cuán complicada sea la curva \(C\), la integral de línea de \(\mathbf{F}\) a lo largo de \(C\) solo puede tener uno de dos valores posibles. Consideramos dos casos: el caso en que \(C\) engloba el origen y el caso en que \(C\) no engloba el origen.
Caso 1: \(C\) no engloba el origen
En este caso, la región encerrada por \(C\) es simplemente conexa porque el único agujero en el dominio de \(\mathbf{F}\) está en el origen. Mostramos en nuestra discusión sobre las parciales cruzadas que \(\mathbf{F}\) satisface la condición de parciales cruzadas. Si restringimos el dominio de \(\mathbf{F}\) solo a \(C\) y la región que encierra, entonces \(\mathbf{F}\) con este dominio restringido ahora está definido en un dominio simplemente conexo. Como \(\mathbf{F}\) satisface la propiedad de parciales cruzadas en su dominio restringido, el campo \(\mathbf{F}\) es conservativo en esta región simplemente conexa y, por lo tanto, la circulación \(\int_C \mathbf{F} \cdot d\mathbf{r}\) es cero.
Caso 2: \(C\) engloba el origen
En este caso, la región encerrada por \(C\) no es simplemente conexa porque esta región contiene un agujero en el origen. Sea \(C_1\) un círculo de radio \(a\) centrado en el origen de modo que \(C_1\) esté completamente dentro de la región encerrada por \(C\) (Figura 10.15.15). Asignamos a \(C_1\) una orientación en sentido horario.

Figura 10.15.15 Elija el círculo C1 centrado en el origen que esté contenido completamente dentro de C.
Sea \( D \) la región entre \( C_1 \) y \( C \), y \( C \) está orientada en sentido contrario a las manecillas del reloj. Por la versión extendida del teorema de Green,
\[ \begin{aligned} \int_C \mathbf{F} \cdot d\mathbf{r} + \int_{C_1} \mathbf{F} \cdot d\mathbf{r} &= \iint_D Q_x – P_y \, dA \\ &= \iint_D \frac{y^2 – x^2}{(x^2 + y^2)^2} + \frac{y^2 – x^2}{(x^2 + y^2)^2} \, dA \\ &= 0, \end{aligned} \]y por lo tanto,
\[ \int_C \mathbf{F} \cdot d\mathbf{r} = -\int_{C_1} \mathbf{F} \cdot d\mathbf{r}. \]Dado que \( C_1 \) es una curva específica, podemos evaluar \(\int_{C_1} \mathbf{F} \cdot d\mathbf{r}\). Sea
\[ x = a \cos t, \, y = a \sin t, \, 0 \leq t \leq 2\pi \]una parametrización de \( C_1 \). Entonces,
\[ \begin{aligned} \int_{C_1} \mathbf{F} \cdot d\mathbf{r} &= \int_0^{2\pi} \mathbf{F}(\mathbf{r}(t)) \cdot \mathbf{r}'(t) \, dt \\ &= \int_0^{2\pi} \left( \frac{\sin(t)}{a}, \frac{\cos(t)}{a} \right) \cdot (-a \sin(t), -a \cos(t)) \, dt \\ &= \int_0^{2\pi} \sin^2(t) + \cos^2(t) \, dt \\ &= \int_0^{2\pi} dt \\ &= 2\pi. \end{aligned} \]Por lo tanto, \(\int_C \mathbf{F} \cdot d\mathbf{r} = -2\pi\). ♦
Ejercicio de control 10.15.6
Calcular la integral \(\int_{\partial D} \mathbf{F} \cdot d\mathbf{r}\), donde \(D\) es el anillo dado por las desigualdades polares
\[2 \leq r \leq 5, 0 \leq \theta \leq 2\pi, \text{ y } \mathbf{F}(x, y) = \left\langle x^3, 5x + e^{y}\sin y\right\rangle.\] ♦
