| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.18 |

10.18 Teorema de Stokes

Objetivos de aprendizaje:

10.18.1 Explicar el significado del teorema de Stokes.
10.18.2 Usar el teorema de Stokes para evaluar una integral de línea.
10.18.3 Usar el teorema de Stokes para calcular una integral de superficie.
10.18.4 Usar el teorema de Stokes para calcular un rotacional.

En esta sección, estudiamos el teorema de Stokes, una generalización en dimensiones superiores del teorema de Green. Este teorema, al igual que el Teorema Fundamental de los Integrales de Línea y el teorema de Green, es una extensión del Teorema Fundamental del Cálculo a dimensiones superiores. El teorema de Stokes relaciona una integral de superficie de un campo vectorial sobre una superficie S en el espacio con una integral de línea alrededor del borde de S. Por lo tanto, al igual que los teoremas anteriores, el teorema de Stokes puede utilizarse para reducir una integral sobre un objeto geométrico S a una integral sobre su borde.

Además de permitirnos traducir entre integrales de línea e integrales de superficie, el teorema de Stokes conecta los conceptos de rotacional y circulación. Asimismo, el teorema tiene aplicaciones en la mecánica de fluidos y el electromagnetismo. Utilizamos el teorema de Stokes para derivar la ley de Faraday, un resultado importante relacionado con los campos eléctricos.

Teorema de Stokes

El teorema de Stokes establece que podemos calcular el flujo del rotacional de F a través de la superficie S conociendo únicamente los valores de F a lo largo del borde de S. De manera inversa, podemos calcular la integral de línea del campo vectorial F a lo largo del borde de la superficie S traduciéndola a una integral doble del rotacional de F sobre S.

Sea S una superficie suave y orientada con vector normal unitario N. Además, supongamos que el borde de S es una curva cerrada simple C. La orientación de S induce la orientación positiva de C si, al caminar en la dirección positiva alrededor de C con la cabeza apuntando en la dirección de N, la superficie siempre queda a la izquierda. Con esta definición, podemos enunciar el teorema de Stokes.

Teorema 10.18.1: Teorema de Stokes

Sea \( S \) una superficie orientada suave por partes con un borde que es una curva cerrada simple \( C \) con orientación positiva (Figura 10.18.1). Si \( \mathbf{F} \) es un campo vectorial cuyas funciones componentes tienen derivadas parciales continuas en una región abierta que contiene \( S \), entonces

\[ \int_C \mathbf{F} \cdot d\mathbf{r} = \iint_S \operatorname{curl} \mathbf{F} \cdot d\mathbf{S}. \]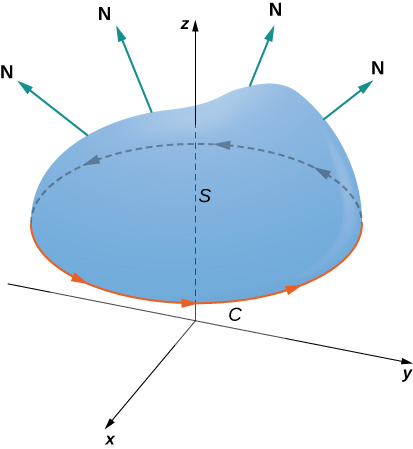

Figura 10.18.1 El teorema de Stokes relaciona la integral de flujo sobre la superficie con una integral de línea alrededor del borde de la superficie. Nótese que la orientación de la curva es positiva. ♦

Suponga que la superficie \(S\) es una región plana en el plano xy con orientación hacia arriba. Entonces el vector normal unitario es \(\mathbf{k}\) y la integral de superficie \(\iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S}\) es en realidad la integral doble \(\iint_S \text{rot} \, \mathbf{F} \cdot \mathbf{k} \, dA\). En este caso especial, el teorema de Stokes da

\[ \oint_C \mathbf{F} \cdot d\mathbf{r} = \iint_S \text{rot} \, \mathbf{F} \cdot \mathbf{k} \, dA. \]

Sin embargo, esta es la forma de circulación del teorema de Green, lo que nos muestra que el teorema de Green es un caso especial del teorema de Stokes. El teorema de Green solo puede manejar superficies en un plano, pero el teorema de Stokes puede manejar superficies en un plano o en el espacio.

La prueba completa del teorema de Stokes está fuera del alcance de este texto. Examinamos una explicación intuitiva de la verdad del teorema y luego vemos la prueba del teorema en el caso especial en que la superficie \(S\) es una porción de la gráfica de una función, y \(S\), el límite de \(S\) y \(\mathbf{F}\) son todos razonablemente bien comportados.

Prueba:

Primero, echamos un vistazo a una prueba informal del teorema. Esta prueba no es rigurosa, pero tiene como objetivo dar una idea general de por qué el teorema es cierto. Sea \(S\) una superficie y sea \(D\) una pequeña pieza de la superficie de modo que \(D\) no comparta ningún punto con la frontera de \(S\). Elegimos \(D\) para que sea lo suficientemente pequeño para que pueda ser aproximado por un cuadrado orientado \(E\). Sea \(D\) herede su orientación de \(S\), y dé a \(E\) la misma orientación. Este cuadrado tiene cuatro lados; denotémoslos \(E_l\), \(E_r\), \(E_u\) y \(E_d\) para los lados izquierdo, derecho, superior e inferior, respectivamente. En el cuadrado, podemos usar la forma de flujo del teorema de Green:

\[ \oint_{E_l + E_d + E_r + E_u} \mathbf{F} \cdot d\mathbf{r} = \iint_E \text{rot} \, \mathbf{F} \cdot \mathbf{N} \, dS = \iint_E \text{rot} \, \mathbf{F} \cdot d\mathbf{S}. \]

Para aproximar el flujo sobre toda la superficie, sumamos los valores del flujo en los cuadrados pequeños que aproximan la superficie (Figura 10.18.2). Por el teorema de Green, el flujo a través de cada cuadrado de aproximación es una integral de línea sobre su frontera. Sea \(F\) un cuadrado de aproximación con una orientación heredada de \(S\) y con un lado derecho \(E_l\) (de modo que \(F\) esté a la izquierda de \(E\)). Sea \(F_r\) denote el lado derecho de \(F\); entonces, \(E_l = -F_r\). En otras palabras, el lado derecho de \(F\) es la misma curva que el lado izquierdo de \(E\), solo que orientada en la dirección opuesta. Por lo tanto,

\[ \oint_{E_l} \mathbf{F} \cdot d\mathbf{r} = – \oint_{F_r} \mathbf{F} \cdot d\mathbf{r}. \]

A medida que sumamos todos los flujos sobre todos los cuadrados que aproximan la superficie \(S\), las integrales de línea \(\oint_{E_l} \mathbf{F} \cdot d\mathbf{r}\) y \(\oint_{F_r} \mathbf{F} \cdot d\mathbf{r}\) se cancelan entre sí. Lo mismo ocurre con las integrales de línea sobre los otros tres lados de \(E\). Estas tres integrales de línea se cancelan con la integral de línea del lado inferior del cuadrado sobre \(E\), la integral de línea del lado izquierdo del cuadrado a la derecha de \(E\), y la integral de línea sobre el lado superior del cuadrado debajo de \(E\) (Figura 10.18.3). Después de que toda esta cancelación ocurre sobre todos los cuadrados de aproximación, las únicas integrales de línea que sobreviven son las integrales de línea sobre los lados que aproximan la frontera de \(S\). Por lo tanto, la suma de todos los flujos (que, por el teorema de Green, es la suma de todas las integrales de línea alrededor de las fronteras de los cuadrados de aproximación) puede aproximarse mediante una integral de línea sobre la frontera de \(S\). En el límite, a medida que las áreas de los cuadrados de aproximación se acercan a cero, esta aproximación se acerca arbitrariamente al flujo.

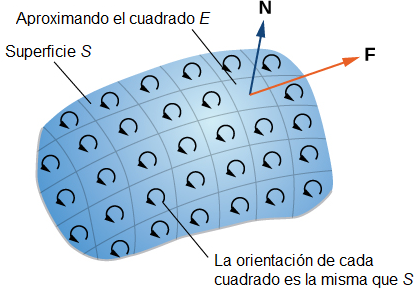
Figura 10.18.2 Cortar la superficie en trozos pequeños. Los trozos deben ser lo suficientemente pequeños como para que puedan ser aproximados por un cuadrado.

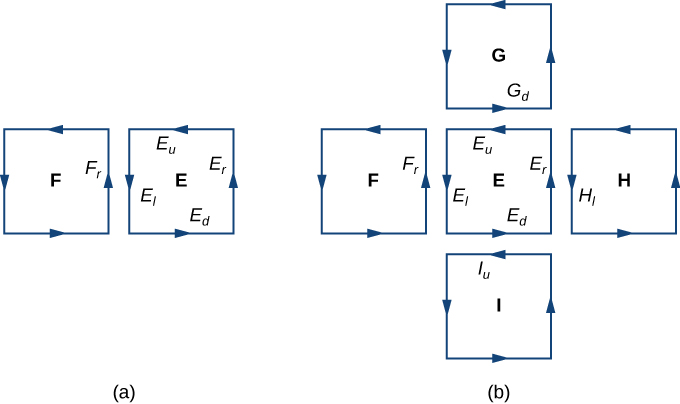
Figura 10.18.3 (a) La integral de línea a lo largo de \(\underline{E}_{I}\) cancela la integral de línea a lo largo de \(F_{r}\) porque \(\underline{E}_{I} = -F_{r}\). (b) La integral de línea a lo largo de cualquier lado de \(E\) se cancela con la integral de línea a lo largo de un lado de un cuadrado de aproximación adyacente.

Veamos ahora una prueba rigurosa del teorema en el caso especial en que \(S\) es la gráfica de la función \(z = f(x, y)\), donde \(x\) e \(y\) varían sobre una región \(D\) acotada y simplemente conexa de área finita (Figura 10.18.4). Además, supongamos que \(f\) tiene derivadas parciales continuas de segundo orden. Sea \(C\) denote la frontera de \(S\) y sea \(C’\) denote la frontera de \(D\). Entonces, \(D\) es la “sombra” de \(S\) en el plano y \(C’\) es la “sombra” de \(C\). Supongamos que \(S\) está orientada hacia arriba. La orientación en sentido antihorario de \(C\) es positiva, al igual que la orientación en sentido antihorario de \(C’\). Sea \(\mathbf{F}(x, y, z) = \langle P, Q, R \rangle\) un campo vectorial con funciones componentes que tienen derivadas parciales continuas.

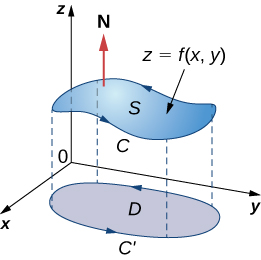
Figura 10.18.4 D es la “sombra”, o proyección, de S en el plano y C′ es la proyección de C.

Tomamos la parametrización estándar de \(S\): \(x = x\), \(y = y\), \(z = g(x, y)\). Los vectores tangentes son \(\mathbf{t}_x = \langle 1, 0, g_x \rangle\) y \(\mathbf{t}_y = \langle 0, 1, g_y \rangle\), y por lo tanto \(\mathbf{t}_x \times \mathbf{t}_y = \langle -g_x, -g_y, 1 \rangle\). Por la Ecuación 10.17.1,

\[ \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S} = \iint_D \left[ -(R_y – Q_z) z_x – (P_z – R_x) z_y + (Q_x – P_y) \right] dA, \]

donde las derivadas parciales se evalúan en \((x, y, g(x, y))\), haciendo que el integrando dependa solo de \(x\) e \(y\). Supongamos que \((x(t), y(t)), a \leq t \leq b\) es una parametrización de \(C’\). Entonces, una parametrización de \(C\) es \((x(t), y(t), g(x(t), y(t))), a \leq t \leq b\). Armados con estas parametrizaciones, la regla de la cadena y el teorema de Green, y teniendo en cuenta que \(P\), \(Q\) y \(R\) son todas funciones de \(x\) e \(y\), podemos evaluar la integral de línea \(\oint_C \mathbf{F} \cdot d\mathbf{r}\):

\[ \begin{aligned} \oint_C \mathbf{F} \cdot d\mathbf{r} &= \int_a^b \left( Px'(t) + Qy'(t) + Rz'(t) \right) dt \\ &= \int_a^b \left[ Px'(t) + Qy'(t) + R \left( \frac{\partial z}{\partial x} \frac{dx}{dt} + \frac{\partial z}{\partial y} \frac{dy}{dt} \right) \right] dt \\ &= \int_a^b \left[ \left( P + R \frac{\partial z}{\partial x} \right) x'(t) + \left( Q + R \frac{\partial z}{\partial y} \right) y'(t) \right] dt \\ &= \oint_{C’} \left( P + R \frac{\partial z}{\partial x} \right) dx + \left( Q + R \frac{\partial z}{\partial y} \right) dy \\ &= \iint_D \left[ \frac{\partial}{\partial x} \left( Q + R \frac{\partial z}{\partial y} \right) – \frac{\partial}{\partial y} \left( P + R \frac{\partial z}{\partial x} \right) \right] dA \\ &= \iint_D \left[ \left( \frac{\partial Q}{\partial x} + \frac{\partial Q}{\partial z} \frac{\partial z}{\partial x} + \frac{\partial R}{\partial x} \frac{\partial z}{\partial y} + R \frac{\partial^2 z}{\partial x \partial y} \right) – \left( \frac{\partial P}{\partial y} + \frac{\partial P}{\partial z} \frac{\partial z}{\partial y} + \frac{\partial R}{\partial y} \frac{\partial z}{\partial x} + R \frac{\partial^2 z}{\partial y \partial x} \right) \right] dA. \end{aligned} \]

Por el teorema de Clairaut, \(\frac{\partial^2 z}{\partial x \partial y} = \frac{\partial^2 z}{\partial y \partial x}\). Por lo tanto, cuatro de los términos desaparecen de esta integral doble, y nos quedamos con

\[ \iint_D \left[ -(R_y – Q_z) z_x – (P_z – R_x) z_y + (Q_x – P_y) \right] dA, \]

lo que es igual a \(\iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S}\). ♦

Hemos demostrado que el teorema de Stokes es cierto en el caso de una función con un dominio que es una región simplemente conexa de área finita. Podemos confirmar rápidamente este teorema para otro caso importante: cuando el campo vectorial \(\mathbf{F}\) es conservativo. Si \(\mathbf{F}\) es conservativo, el rotacional de \(\mathbf{F}\) es cero, por lo que \(\displaystyle \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S} = 0\). Dado que la frontera de \(S\) es una curva cerrada, \(\oint_C \mathbf{F} \cdot d\mathbf{r}\) también es cero.

Ejemplo ilustrativo 10.18.1: Verificando el Teorema de Stokes para un Caso Específico

Verifique que el teorema de Stokes es cierto para el campo vectorial \(\mathbf{F}(x, y, z) = \langle y, 2z, x^2 \rangle\) y la superficie \(S\), donde \(S\) es el paraboloide \(z = 4 – x^2 – y^2\). Asuma que la superficie está orientada hacia afuera y que \(z \geq 0\).

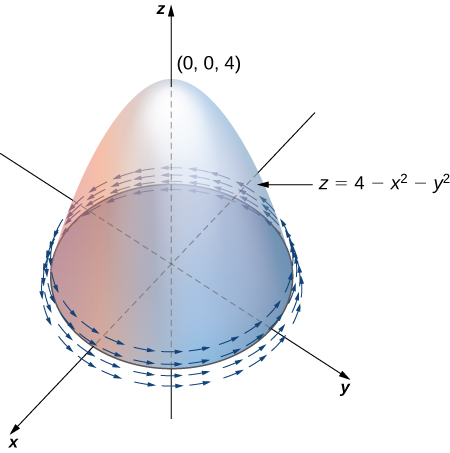
Figura 10.18.5 Verificando el teorema de Stokes para un hemisferio en un campo vectorial.

Solución:

Como una integral de superficie, tienes \(g(x, y) = 4 – x^2 – y^2\), \(g_x = -2x\) y \(g_y = -2y\)

\[ \text{rot} \, \mathbf{F} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ y & 2z & x^2 \end{vmatrix} = \langle -2, -2x, -1 \rangle. \]

Por la Ecuación 10.17.1,

\[ \begin{aligned} \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S} &= \iint_D \text{rot} \, \mathbf{F}(\mathbf{r}(\phi, \theta)) \cdot (\mathbf{t}_\phi \times \mathbf{t}_\theta) \, dA \\ &= \iint_D \langle -2, -2x, -1 \rangle \cdot \langle 2x, 2y, 1 \rangle \, dA \\ &= \int_{-2}^{2} \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} (-4x – 4xy – 1) \, dy \, dx \\ &= \int_{-2}^{2} (-8x \sqrt{4 – x^2} – 2 \sqrt{4 – x^2}) \, dx \\ &= -4\pi. \end{aligned} \]

Como una integral de línea, puedes parametrizar \(C\) por \(\mathbf{r}(t) = \langle 2 \cos t, 2 \sin t, 0 \rangle\), \(0 \leq t \leq 2\pi\). Por la Ecuación 10.17.1,

\[ \oint_C \mathbf{F} \cdot d\mathbf{r} = \int_{0}^{2\pi} \langle 2 \sin t, 0, 4 \cos^2 t \rangle \cdot \langle -2 \sin t, 2 \cos t, 0 \rangle \, dt = \int_{0}^{2\pi} -4 \sin^2 t \, dt = -4\pi. \hspace{20pt} \text{(Ecuación 10.18.1)} \]

Por lo tanto, hemos verificado el teorema de Stokes para este ejemplo. ♦

Ejercicio de control 10.18.1

Verifique que el teorema de Stokes es cierto para el campo vectorial \(\mathbf{F}(x, y, z) = \langle y, x, -z \rangle\) y la superficie \(S\), donde \(S\) es la porción orientada hacia arriba de la gráfica de \(f(x, y) = x^2 y\) sobre un triángulo en el plano xy con vértices \((0, 0)\), \((2, 0)\) y \((0, 2)\). ♦

Aplicando el Teorema de Stokes

El teorema de Stokes traduce entre la integral de flujo de la superficie S a una integral de línea alrededor de la frontera de S. Por lo tanto, el teorema nos permite calcular integrales de superficie o integrales de línea que normalmente serían bastante difíciles traduciendo la integral de línea en una integral de superficie o viceversa. Ahora estudiamos algunos ejemplos de cada tipo de traducción.

Ejemplo ilustrativo 10.18.2: Calculando una Integral de Superficie

Calcular la integral de superficie \(\displaystyle \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S}\), donde \(S\) es la superficie, orientada hacia afuera, en la Figura 10.18.6 y \(\mathbf{F} = \langle z, 2xy, x + y \rangle\).

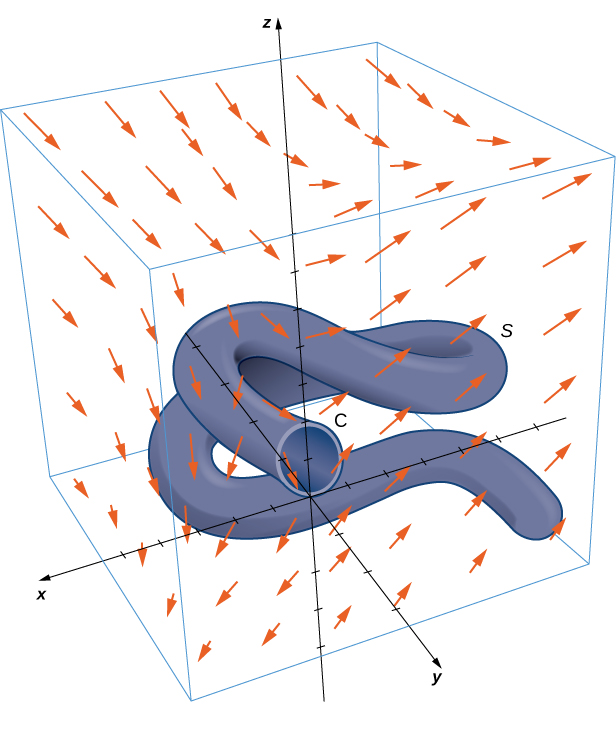
Figura 10.18.6 Una superficie complicada en un campo vectorial.

Solución:

Tenga en cuenta que para calcular \(\displaystyle \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S}\) sin usar el teorema de Stokes, necesitaríamos usar la Ecuación 10.17.1. El uso de esta ecuación requiere una parametrización de \(S\). La superficie \(S\) es lo suficientemente complicada como para que sea extremadamente difícil encontrar una parametrización. Por lo tanto, los métodos que hemos aprendido en secciones anteriores no son útiles para este problema. En cambio, usamos el teorema de Stokes, notando que la frontera \(C\) de la superficie es simplemente un círculo con radio 1.

El rotacional de \(\mathbf{F}\) es \(\langle 1, 0, 2y \rangle\). Por el teorema de Stokes,

\[ \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S} = \oint_C \mathbf{F} \cdot d\mathbf{r}, \]

donde \(C\) tiene parametrización \(\mathbf{r}(t) = \langle \sin t, 0, 1 – \cos t \rangle\), \(0 \leq t < 2\pi\). Por la Ecuación 10.17.1,

\[ \begin{aligned} \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S} &= \oint_C \mathbf{F} \cdot d\mathbf{r} \\ &= \int_0^{2\pi} \langle 1 – \cos t, 0, -\sin t \rangle \cdot \langle \sin t, 0, \cos t \rangle \, dt \\ &= \int_0^{2\pi} (\sin t – \sin t \cos t) \, dt \\ &= \int_0^{2\pi} \left(\sin t – \frac{1}{2} \sin 2t \right) dt \\ &= \left[ -\cos t – \frac{1}{4} \cos 2t \right]_0^{2\pi} \\ &= \left[ -\cos 2\pi – \frac{1}{4} \cos 4\pi \right] – \left[ -\cos 0 – \frac{1}{4} \cos 0 \right] \\ &= 0. \end{aligned} \]

♦

Una consecuencia sorprendente del teorema de Stokes es que si \(S’\) es cualquier otra superficie suave con frontera \(C\) y la misma orientación que \(S\), entonces \(\displaystyle \iint_{S’} \text{rot} \, \mathbf{F} \cdot d\mathbf{S} = \oint_C \mathbf{F} \cdot d\mathbf{r}\) porque el teorema de Stokes dice que la integral de superficie depende solo de la integral de línea alrededor de la frontera.

En el Ejemplo 10.18.2, calculamos una integral de superficie simplemente usando información sobre la frontera de la superficie. En general, sean \(S_1\) y \(S_2\) superficies suaves con la misma frontera \(C\) y la misma orientación. Por el teorema de Stokes,

\[ \iint_{S_1} \text{rot} \, \mathbf{F} \cdot d\mathbf{S} = \oint_C \mathbf{F} \cdot d\mathbf{r} = \iint_{S_2} \text{rot} \, \mathbf{F} \cdot d\mathbf{S}. \hspace{20pt} \text{(Ecuación 10.18.2)} \]

Por lo tanto, si \(\displaystyle \iint_{S_1} \text{rot} \, \mathbf{F} \cdot d\mathbf{S}\) es difícil de calcular pero \(\displaystyle \iint_{S_2} \text{rot} \, \mathbf{F} \cdot d\mathbf{S}\) es fácil de calcular, el teorema de Stokes nos permite calcular la integral de superficie más fácil. En el Ejemplo 10.18.2, podríamos haber calculado \(\displaystyle \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S}\) calculando \(\displaystyle \iint_{S’} \text{rot} \, \mathbf{F} \cdot d\mathbf{S}\), donde \(S’\) es el disco encerrado por la curva de la frontera \(C\) (una superficie mucho más simple con la que trabajar).

La Ecuación 10.18.2 muestra que las integrales de flujo de campos vectoriales rotacionales son independientes de la superficie de la misma manera que las integrales de línea de campos de gradiente son independientes del camino. Recuerde que si F es un campo vectorial conservativo bidimensional definido en un dominio simplemente conexo, \(f\) es una función potencial para F, y \(C\) es una curva en el dominio de F, entonces \(\oint_C \mathbf{F} \cdot d\mathbf{r}\) depende solo de los puntos finales de \(C\). Por lo tanto, si \(C’\) es cualquier otra curva con el mismo punto de inicio y el mismo punto final que \(C\) (es decir, \(C’\) tiene la misma orientación que \(C\)), entonces \(\oint_C \mathbf{F} \cdot d\mathbf{r} = \oint_{C’} \mathbf{F} \cdot d\mathbf{r}\). En otras palabras, el valor de la integral depende de la frontera del camino solamente; realmente no depende del camino en sí.

Análogamente, suponga que \(S\) y \(S’\) son superficies con la misma frontera y la misma orientación, y suponga que \(\mathbf{G}\) es un campo vectorial tridimensional que se puede escribir como el rotacional de otro campo vectorial \(\mathbf{F}\) (de modo que \(\mathbf{F}\) es como un “campo potencial” de \(\mathbf{G}\)). Por la Ecuación 10.18.2,

\[ \iint_S \mathbf{G} \cdot d\mathbf{S} = \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S} = \oint_C \mathbf{F} \cdot d\mathbf{r} = \iint_{S’} \text{rot} \, \mathbf{F} \cdot d\mathbf{S} = \iint_{S’} \mathbf{G} \cdot d\mathbf{S}. \]

Por lo tanto, la integral de flujo de \(\mathbf{G}\) no depende de la superficie, sino solo de la frontera de la superficie. Las integrales de flujo de campos vectoriales que se pueden escribir como el rotacional de un campo vectorial son independientes de la superficie de la misma manera que las integrales de línea de campos vectoriales que se pueden escribir como el gradiente de una función escalar son independientes del camino.

Ejercicio de control 10.18.2

Use el teorema de Stokes para calcular la integral de superficie \(\displaystyle \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S}\), donde \(\mathbf{F} = \langle z, x, y \rangle\) y \(S\) es la superficie como se muestra en la siguiente figura. La curva de la frontera, \(C\), está orientada en sentido horario cuando se mira a lo largo del eje y positivo.

♦

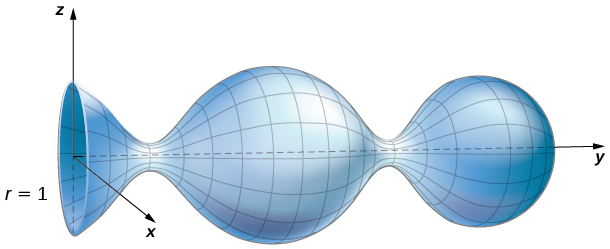
Ejemplo ilustrativo 10.18.3: Calculando una Integral de Línea

Calcular la integral de línea \(\oint_C \mathbf{F} \cdot d\mathbf{r}\), donde \(\mathbf{F} = \langle xy, x^2 + y^2 + z^2, yz \rangle\) y \(C\) es la frontera del paralelogramo con vértices \((0, 0, 1)\), \((0, 1, 0)\), \((2, 0, -1)\) y \((2, 1, -2)\).

Solución:

Para calcular la integral de línea directamente, necesitamos parametrizar cada lado del paralelogramo por separado, calcular cuatro integrales de línea separadas y sumar el resultado. Esto no es demasiado complicado, pero requiere mucho tiempo.

Por el contrario, calculemos la integral de línea usando el teorema de Stokes. Sea \(S\) denote la superficie del paralelogramo. Note que \(S\) es la porción de la gráfica de \(z = 1 – x – y\) para \((x, y)\) variando sobre la región rectangular con vértices \((0, 0)\), \((0, 1)\), \((2, 0)\) y \((2, 1)\) en el plano xy. Por lo tanto, una parametrización de \(S\) es \(\langle x, y, 1 – x – y \rangle\), \(0 \leq x \leq 2\), \(0 \leq y \leq 1\). El rotacional de \(\mathbf{F}\) es \(\langle -z, 0, x \rangle\), y el teorema de Stokes y la Ecuación 10.17.1 dan

\[ \begin{aligned} \oint_C \mathbf{F} \cdot d\mathbf{r} &= \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S} \\ &= \int_0^2 \int_0^1 \text{rot} \, \mathbf{F}(x, y) \cdot (\mathbf{t}_x \times \mathbf{t}_y) \, dy \, dx \\ &= \int_0^2 \int_0^1 \langle -(1 – x – y), 0, x \rangle \cdot (\langle 1, 0, -1 \rangle \times \langle 0, 1, -1 \rangle) \, dy \, dx \\ &= \int_0^2 \int_0^1 \langle x + y – 1, 0, x \rangle \cdot \langle 1, 1, 1 \rangle \, dy \, dx \\ &= \int_0^2 \int_0^1 (2x + y – 1) \, dy \, dx \\ &= 3. \end{aligned} \]

♦

Ejercicio de control 10.18.3

Use el teorema de Stokes para calcular la integral de línea \(\oint_C \mathbf{F} \cdot d\mathbf{r}\), donde \(\mathbf{F} = \langle z, x, y \rangle\) y \(C\) está orientada en sentido horario y es la frontera de un triángulo con vértices \((0, 0, 1)\), \((3, 0, -2)\) y \((0, 1, 2)\). ♦

Interpretación del Rotacional

Además de permitirnos traducir entre integrales de línea e integrales de flujo, el teorema de Stokes se puede usar para justificar la interpretación física del rotacional que hemos aprendido. Aquí investigamos la relación entre el rotacional y la circulación, y usamos el teorema de Stokes para enunciar la ley de Faraday, una ley importante en electricidad y magnetismo que relaciona el rotacional de un campo eléctrico con la tasa de cambio de un campo magnético.

Recordemos que si \(C\) es una curva cerrada y \(\mathbf{F}\) es un campo vectorial definido en \(C\), entonces la circulación de \(\mathbf{F}\) alrededor de \(C\) es la integral de línea \(\oint_C \mathbf{F} \cdot d\mathbf{r}\). Si \(\mathbf{F}\) representa el campo de velocidad de un fluido en el espacio, entonces la circulación mide la tendencia del fluido a moverse en la dirección de \(C\).

Sea \(\mathbf{F}\) un campo vectorial continuo y sea \(D_r\) un disco pequeño de radio \(r\) con centro \(P_0\) (Figura 10.18.7). Si \(D_r\) es lo suficientemente pequeño, entonces \((\text{rot} \, \mathbf{F})(P) \approx (\text{rot} \, \mathbf{F})(P_0)\) para todos los puntos \(P\) en \(D_r\) porque el rotacional es continuo. Sea \(C_r\) el círculo de la frontera de \(D_r\). Por el teorema de Stokes,

\[ \oint_{C_r} \mathbf{F} \cdot d\mathbf{r} = \iint_{D_r} \text{rot} \, \mathbf{F} \cdot \mathbf{N} \, dS \approx \iint_{D_r} (\text{rot} \, \mathbf{F})(P_0) \cdot \mathbf{N}(P_0) \, dS. \]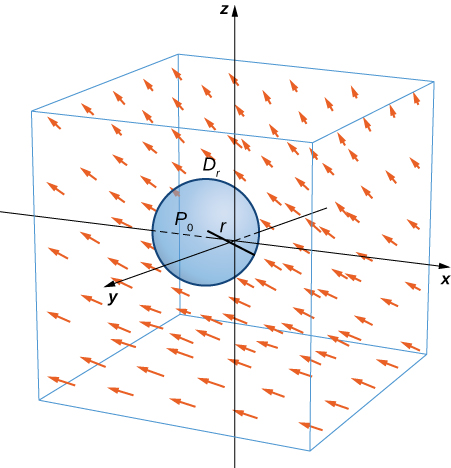

Figura 10.18.7 El disco D_r es un disco pequeño en un campo vectorial continuo.

La cantidad \((\text{rot} \, \mathbf{F})(P_0) \cdot \mathbf{N}(P_0)\) es constante, y por lo tanto

\[ \iint_{D_r} (\text{rot} \, \mathbf{F})(P_0) \cdot \mathbf{N}(P_0) \, dS = \pi r^2 [(\text{rot} \, \mathbf{F})(P_0) \cdot \mathbf{N}(P_0)]. \]

Así,

\[ \oint_{C_r} \mathbf{F} \cdot d\mathbf{r} \approx \pi r^2 [(\text{rot} \, \mathbf{F})(P_0) \cdot \mathbf{N}(P_0)], \]

y la aproximación se acerca arbitrariamente a medida que el radio se reduce a cero. Por lo tanto, el teorema de Stokes implica que

\[ (\text{rot} \, \mathbf{F})(P_0) \cdot \mathbf{N}(P_0) = \lim_{r \to 0^+} \frac{1}{\pi r^2} \oint_{C_r} \mathbf{F} \cdot d\mathbf{r}. \]

Esta ecuación relaciona el rotacional de un campo vectorial con la circulación. Dado que el área del disco es \(\pi r^2\), esta ecuación dice que podemos ver el rotacional (en el límite) como la circulación por unidad de área. Recordemos que si \(\mathbf{F}\) es el campo de velocidad de un fluido, entonces la circulación \(\oint_{C_r} \mathbf{F} \cdot d\mathbf{r} = \oint_{C_r} \mathbf{F} \cdot \mathbf{T} \, ds\) es una medida de la tendencia del fluido a moverse alrededor de \(C_r\). La razón de esto es que \(\mathbf{F} \cdot \mathbf{T}\) es un componente de \(\mathbf{F}\) en la dirección de \(\mathbf{T}\), y cuanto más se acerca la dirección de \(\mathbf{F}\) a \(\mathbf{T}\), mayor es el valor de \(\mathbf{F} \cdot \mathbf{T}\) (recuerde que si \(\mathbf{a}\) y \(\mathbf{b}\) son vectores y \(\mathbf{b}\) es fijo, entonces el producto punto \(\mathbf{a} \cdot \mathbf{b}\) es máximo cuando \(\mathbf{a}\) apunta en la misma dirección que \(\mathbf{b}\)). Por lo tanto, si \(\mathbf{F}\) es el campo de velocidad de un fluido, entonces \(\text{rot} \, \mathbf{F} \cdot \mathbf{N}\) es una medida de cómo el fluido gira alrededor del eje \(\mathbf{N}\). El efecto del rotacional es más grande sobre el eje que apunta en la dirección de \(\mathbf{N}\), porque en este caso \(\text{rot} \, \mathbf{F} \cdot \mathbf{N}\) es lo más grande posible.

Para ver este efecto de una manera más concreta, imagine colocar una pequeña rueda de paletas en el punto \(P_0\) (Figura 10.18.8). La rueda de paletas alcanza su velocidad máxima cuando el eje de la rueda apunta en la dirección de \(\text{rot} \, \mathbf{F}\). Esto justifica la interpretación del rotacional que hemos aprendido: el rotacional es una medida de la rotación en el campo vectorial sobre el eje que apunta en la dirección del vector normal \(\mathbf{N}\), y el teorema de Stokes justifica esta interpretación.

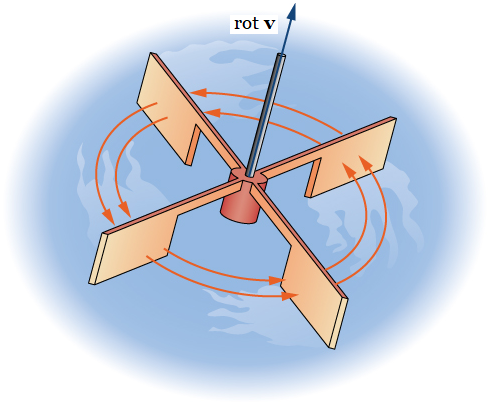
Figura 10.18.8 Para visualizar el rotacional en un punto, imagine colocar una pequeña rueda de paletas en ese punto en el campo vectorial.

Ahora que hemos aprendido sobre el teorema de Stokes, podemos discutir aplicaciones en el área del electromagnetismo. En particular, examinaremos cómo podemos usar el teorema de Stokes para traducir entre dos formas equivalentes de la ley de Faraday. Antes de enunciar las dos formas de la ley de Faraday, necesitamos algo de terminología básica.

Sea \(C\) una curva cerrada que modela un alambre delgado. En el contexto de los campos eléctricos, el alambre puede estar moviéndose con el tiempo, por lo que escribimos \(C(t)\) para representar el alambre. En un tiempo \(t\) dado, la curva \(C(t)\) puede ser diferente de la curva original \(C\), pero asumimos que \(C(t)\) es una curva cerrada para todo \(t\). Sea \(D(t)\) una superficie con \(C(t)\) como su frontera, y orientamos \(C(t)\) de modo que \(D(t)\) tenga una orientación positiva. Supongamos que \(C(t)\) está en un campo magnético \(\mathbf{B}(x, y, z)\) que también puede cambiar con el tiempo. En otras palabras, \(\mathbf{B}\) tiene la forma

\[ \mathbf{B}(x, y, z) = \langle P(x, y, z, t), Q(x, y, z, t), R(x, y, z, t) \rangle, \]

donde \(P\), \(Q\) y \(R\) pueden variar continuamente con el tiempo. Podemos producir corriente a lo largo del alambre cambiando el campo magnético \(\mathbf{B}(t)\) (esto es una consecuencia de la ley de Ampère). El flujo \(\phi(t) = \iint_{D(t)} \mathbf{B}(t) \cdot d\mathbf{S}\) crea el campo eléctrico \(\mathbf{E}(t)\) que realiza trabajo. La forma integral de la ley de Faraday establece que

\[ \text{Trabajo} = \oint_{C(t)} \mathbf{E}(t) \cdot d\mathbf{r} = -\frac{d\phi}{dt}. \]

En otras palabras, el trabajo realizado por \(\mathbf{E}\) es la integral de línea alrededor de la frontera, que también es igual a la tasa de cambio del flujo con respecto al tiempo. La forma diferencial de la ley de Faraday establece que

\[ \text{rot} \, \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}. \]

Usando el teorema de Stokes, podemos mostrar que la forma diferencial de la ley de Faraday es una consecuencia de la forma integral. Por el teorema de Stokes, podemos convertir la integral de línea en la forma integral en una integral de superficie:

\[ -\frac{d\phi}{dt} = \oint_{C(t)} \mathbf{E}(t) \cdot d\mathbf{r} = \iint_{D(t)} \text{rot} \, \mathbf{E}(t) \cdot d\mathbf{S}. \]

Dado que \(\phi(t) = \iint_{D(t)} \mathbf{B}(t) \cdot d\mathbf{S}\), entonces siempre que la integración de la superficie no varíe con el tiempo también tenemos

\[ \frac{d\phi}{dt} = \iint_{D(t)} \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S}. \]

Por lo tanto,

\[ \iint_{D(t)} -\frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S} = \iint_{D(t)} \text{rot} \, \mathbf{E} \cdot d\mathbf{S}. \]

Para derivar la forma diferencial de la ley de Faraday, nos gustaría concluir que \(\text{rot} \, \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}\). En general, la ecuación

\[ \iint_{D(t)} -\frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S} = \iint_{D(t)} \text{rot} \, \mathbf{E} \cdot d\mathbf{S} \]

no es suficiente para concluir que \(\text{rot} \, \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}\). Los símbolos de la integral no simplemente “se cancelan”, dejando igualdad de los integrandos. Para ver por qué el símbolo de la integral no simplemente se cancela en general, considere las dos integrales de una sola variable \(\int_0^1 x \, dz\) y \(\int_0^1 f(x) \, dx\), donde

\[ f(x) = \begin{cases} 1, & 0 \leq x \leq 1/2 \\ 0, & 1/2 < x < 1. \end{cases} \]

Ambas de estas integrales son iguales a \(\frac{1}{2}\), así que \(\int_0^1 x \, dx = \int_0^1 f(x) \, dx\). Sin embargo, \(x \neq f(x)\). Análogamente, con nuestra ecuación

\[ \iint_{D(t)} -\frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S} = \iint_{D(t)} \text{rot} \, \mathbf{E} \cdot d\mathbf{S}, \]

no podemos simplemente concluir que \(\text{rot} \, \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}\) solo porque sus integrales son iguales. Sin embargo, en nuestro contexto, la ecuación

\[ \iint_{D(t)} -\frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S} = \iint_{D(t)} \text{rot} \, \mathbf{E} \cdot d\mathbf{S} \]

es cierto para cualquier región, por pequeña que sea (esto está en contraste con las integrales de una sola variable que acabamos de discutir). Si \(\mathbf{F}\) y \(\mathbf{G}\) son campos vectoriales tridimensionales tales que \(\iint_S \mathbf{F} \cdot d\mathbf{S} = \iint_S \mathbf{G} \cdot d\mathbf{S}\) para cualquier superficie \(S\), entonces es posible mostrar que \(\mathbf{F} = \mathbf{G}\) al reducir el área de \(S\) a cero tomando un límite (cuanto menor sea el área de \(S\), más cerca estará el valor de \(\iint_S \mathbf{F} \cdot d\mathbf{S}\) al valor de \(\mathbf{F}\) en un punto dentro de \(S\)). Por lo tanto, podemos dejar que el área de \(D(t)\) se reduzca a cero tomando un límite y obtener la forma diferencial de la ley de Faraday:

\[ \text{rot} \, \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}. \]

En el contexto de los campos eléctricos, el rotacional del campo eléctrico puede interpretarse como el negativo de la tasa de cambio del campo magnético correspondiente con respecto al tiempo.

Ejemplo ilustrativo 10.18.4: Usando la Ley de Faraday

Calcule el rotacional del campo eléctrico \(\mathbf{E}\) si el campo magnético correspondiente es un campo constante \(\mathbf{B}(t) = \langle 1, -4, 2 \rangle\).

Solución:

Dado que el campo magnético no cambia con respecto al tiempo, \(-\frac{\partial \mathbf{B}}{\partial t} = \mathbf{0}\). Por la ley de Faraday, el rotacional del campo eléctrico también es cero.

Análisis

Una consecuencia de la ley de Faraday es que el rotacional del campo eléctrico correspondiente a un campo magnético constante es siempre cero. ♦

Ejercicio de control 10.18.4

Calcule el rotacional del campo eléctrico \(\mathbf{E}\) si el campo magnético correspondiente es

\[ \mathbf{B}(t) = \langle tx, ty, -2tz \rangle, \quad 0 \leq t < \infty. \]

Observe que el rotacional del campo eléctrico no cambia con el tiempo, aunque el campo magnético sí cambia con el tiempo. ♦