| 10.17 Integrales de Superficie |

Ejercicios propuestos para el Capítulo 10.17

Para los siguientes ejercicios, determine si las afirmaciones son verdaderas o falsas.

269. Si la superficie \( S \) está dada por \(\{(x, y, z) : 0 \leq x \leq 1, 0 \leq y \leq 1, z = 10\}\), entonces

\[ \iint_S f(x, y, z) \, dS = \int_0^1 \int_0^1 f(x, y, 10) \, dx \, dy. \]

270. Si la superficie \( S \) está dada por \(\{(x, y, z) : 0 \leq x \leq 1, 0 \leq y \leq 1, z = x\}\), entonces

\[ \iint_S f(x, y, z) \, dS = \int_0^1 \int_0^1 f(x, y, x) \, dx \, dy. \]

271. La superficie \( \mathbf{r} = \langle v \cos u, v \sin u, v^2 \rangle \), para \( 0 \leq u \leq \pi, 0 \leq v \leq 2 \), es la misma que la superficie

\[ \mathbf{r} = \langle \sqrt{v} \cos 2u, \sqrt{v} \sin 2u, v \rangle, \text{ para } 0 \leq u \leq \frac{\pi}{2}, 0 \leq v \leq 4. \]

272. Dada la parametrización estándar de una esfera, los vectores normales \( \mathbf{t}_u \times \mathbf{t}_v \) son vectores normales hacia afuera.

Para los siguientes ejercicios, encuentra descripciones paramétricas para las siguientes superficies.

273. Plano \(3x – 2y + z = 2\)

274. Paraboloide \(z = x^{2} + y^{2}\), para \(0 \leq z \leq 9\).

275. Plano \(2x – 4y + 3z = 16\)

276. El tronco de cono \(z^{2} = x^{2} + y^{2}\), para \(2 \leq z \leq 8\)

277. La porción del cilindro \(x^{2} + y^{2} = 9\) en el primer octante, para \(0 \leq z \leq 3\)

278. Un cono con radio de la base \( r \) y altura \( h \), donde \( r \) y \( h \) son constantes positivas.

Para los siguientes ejercicios, usa un sistema de álgebra computacional para aproximar el área de las siguientes superficies usando una descripción paramétrica de la superficie.

279. [T] Medio cilindro \(\{(r, \theta, z): r = 4, 0 \leq \theta \leq \pi, 0 \leq z \leq 7\}\)

280. [T] Plano \(z = 10 – x – y\) sobre el cuadrado \(|x| \leq 2\), \(|y| \leq 2\)

Para los siguientes ejercicios, sea \( S \) el hemisferio \( x^2 + y^2 + z^2 = 4 \), con \( z \geq 0 \), y evalúa cada integral de superficie.

281. \(\displaystyle \iint_S z \, dS\)

282. \(\displaystyle \iint_S (x – 2y) \, dS\)

283. \(\displaystyle \iint_S (x^2 + y^2) z \, dS\)

Para los siguientes ejercicios, evalúa \(\displaystyle \iint_S \mathbf{F} \cdot \mathbf{N} \, dS\) para el campo vectorial \(\mathbf{F}\), donde \(\mathbf{N}\) es un vector normal hacia arriba de la superficie \(S\).

284. \(\mathbf{F}(x, y, z) = x\mathbf{i} + 2y\mathbf{j} – 3z\mathbf{k}\), y \(S\) es la parte del plano \(15x – 12y + 3z = 6\) que se encuentra sobre el cuadrado unitario \(0 \leq x \leq 1, 0 \leq y \leq 1\).

285. \(\mathbf{F}(x, y, z) = x\mathbf{i} + y\mathbf{j}\), y \(S\) es el hemisferio \(z = \sqrt{1 – x^2 – y^2}\).

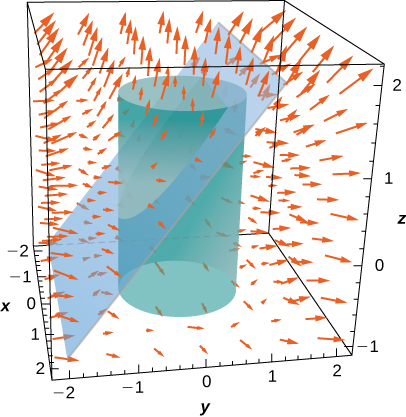
286. \(\mathbf{F}(x, y, z) = x^2\mathbf{i} + y^2\mathbf{j} + z^2\mathbf{k}\), y \(S\) es la porción del plano \(z = y + 1\) que se encuentra dentro del cilindro \(x^2 + y^2 = 1\).

Para los siguientes ejercicios, aproxima la masa de la lámina que tiene la forma de la superficie dada \(S\). Redondea a cuatro decimales.

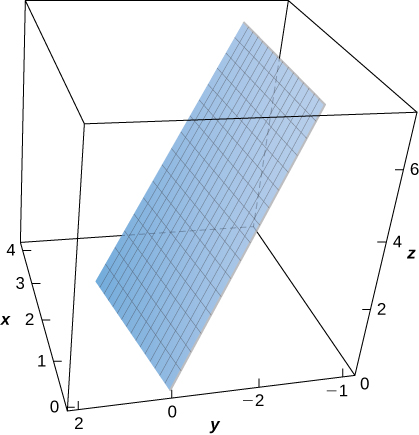
287. [T] \(S\) es la superficie \(z = 4 – x – 2y\), con \(z \geq 0\), \(x \geq 0\), \(y \geq 0\); \(\rho = x\).

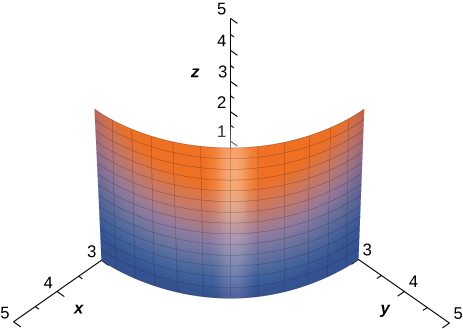
288. [T] \(S\) es la superficie \(z = x^{2} + y^{2}\), con \(z \leq 1\); \(\rho = z\).

289. [T] \(S\) es la superficie \(x^{2} + y^{2} + z^{2} = 5\), con \(z \geq 1\); \(\rho = \theta^{2}\).

290. Evalúa \(\displaystyle \iint_{S} (y^{2}z\mathbf{i} + y^{3}\mathbf{j} + xz\mathbf{k}) \cdot d\mathbf{S}\), donde \(S\) es la superficie del cubo \(-1 \leq x \leq 1\), \(-1 \leq y \leq 1\), y \(0 \leq z \leq 2\). Asume un vector normal hacia afuera.

291. Evalúa la integral de superficie \(\displaystyle \iint_{S} g \, dS\), donde \(g(x, y, z) = xz + 2x^{2} – 3xy\) y \(S\) es la porción del plano \(2x – 3y + z = 6\) que se encuentra sobre el cuadrado unitario \(R\): \(0 \leq x \leq 1\), \(0 \leq y \leq 1\).

292. Evalúa \(\displaystyle \iint_{S} (x^{2} + y – z) \, dS\), donde \(S\) es la superficie definida paramétricamente por \(\mathbf{r}(u, v) = (2u + v)\mathbf{i} + (u – 2v)\mathbf{j} + (u + 3v)\mathbf{k}\) para \(0 \leq u \leq 1\), y \(0 \leq v \leq 2\).

293. [T] Evalúe \(\displaystyle \iint_S (x – y^2 + z) \, dS\), donde S es la superficie definida por

\[ \mathbf{r}(u, v) = u^2 \mathbf{i} + v \mathbf{j} + u \mathbf{k}, 0 \leq u \leq 1, 0 \leq v \leq 1. \]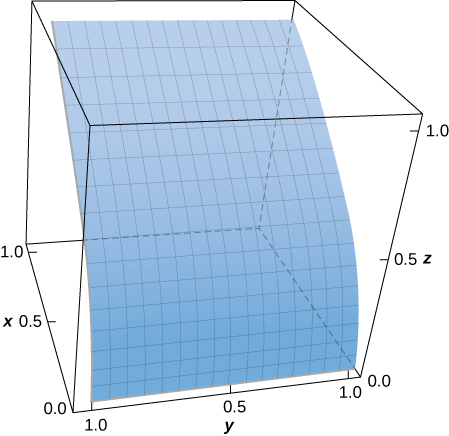

294. [T] Evalúa \(\displaystyle \iint_S \left( x^2 + y^2 – z \right) dS\) donde \(S\) es la superficie definida por

\[ \mathbf{r}(u, v) = u\mathbf{i} – u^3\mathbf{j} + v\mathbf{k}, \, 0 \leq u \leq 2, \, 0 \leq v \leq 1. \]

295. Evalúa \(\displaystyle \iint_S \left( x^2 + y^2 \right) dS\), donde \(S\) es la superficie del hemisferio \(z = \sqrt{1 – x^2 – y^2}\), y por encima del plano \(z = 0\).

296. Evalúa \(\displaystyle \iint_S \left( x^2 + y^2 + z^2 \right) dS\), donde \(S\) es la porción del plano \(z = x + 1\) que se encuentra dentro del cilindro \(x^2 + y^2 = 1\).

297. [T] Evalúa \(\displaystyle \iint_S x^2 z \, dS\), donde \(S\) es la porción del cono \(z^2 = x^2 + y^2\) que se encuentra entre los planos \(z = 1\) y \(z = 4\).

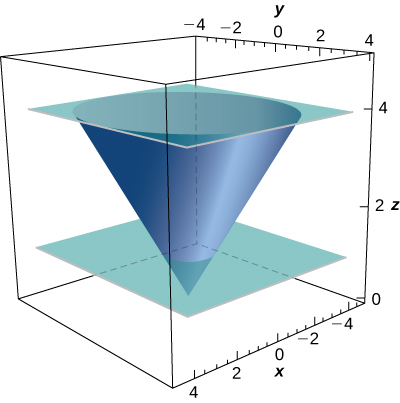
298. [T] Evalúe \(\displaystyle \iint_S \frac{xz}{y} \, dS\), donde S es la porción del cilindro \(x = y^2\) que se encuentra en el primer octante entre los planos \(z = 0\), \(z = 5\), \(y = 1\), y \(y = 4\).

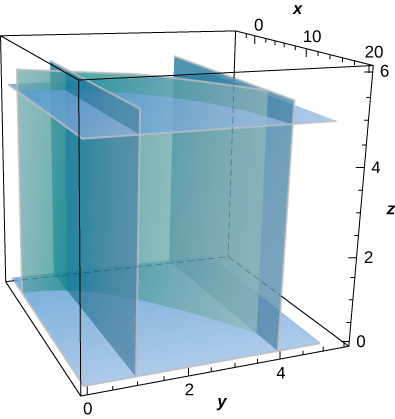
299. [T] Evalúe \(\displaystyle \iint_S (z + y) \, dS\), donde \(S\) es la parte de la gráfica de \(z = \sqrt{1 – x^2}\) en el primer octante entre el plano \(xz\) y el plano \(y = 3\).

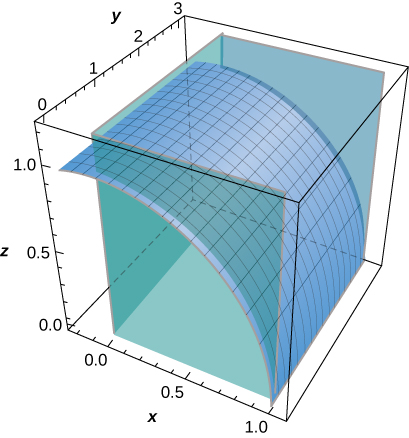
300. Evalúa \(\displaystyle \iint_S xyz \, dS\) si \( S \) es la parte del plano \( z = x + y \) que se encuentra sobre la región triangular en el plano \( xy \) con vértices en \((0, 0, 0)\), \((1, 0, 0)\), y \((0, 2, 0)\).

301. Encuentra la masa de una lámina con densidad \( \rho(x, y, z) = z \) en la forma de un hemisferio \( z = \sqrt{a^2 – x^2 – y^2} \).

302. Calcula \(\displaystyle \int_S \mathbf{F} \cdot \mathbf{N} \, dS\), donde \( \mathbf{F}(x, y, z) = x\mathbf{i} – 5y\mathbf{j} + 4z\mathbf{k} \) y \( \mathbf{N} \) es un vector normal hacia afuera de \( S \), donde \( S \) es la unión de dos cuadrados \( S_1 : x = 0, 0 \leq y \leq 1, 0 \leq z \leq 1 \) y \( S_2 : z = 1, 0 \leq x \leq 1, 0 \leq y \leq 1 \).

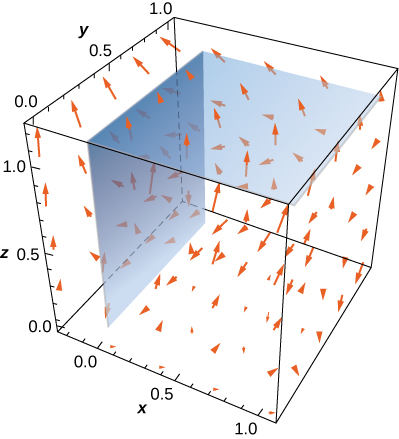
303. Calcula \(\displaystyle \iint_S \mathbf{F} \cdot \mathbf{N} \, dS\), donde \(\mathbf{F}(x, y, z) = xy\mathbf{i} + z\mathbf{j} + (x + y)\mathbf{k}\) y \(\mathbf{N}\) es un vector normal hacia arriba, donde \(S\) es la región triangular del plano \(x + y + z = 1\) en el primer octante.

304. Calcula \(\displaystyle \iint_S \mathbf{F} \cdot \mathbf{N} \, dS\), donde \(\mathbf{F}(x, y, z) = 2yz\mathbf{i} + (\tan^{-1}(xz))\mathbf{j} + e^{xy}\mathbf{k}\) y \(\mathbf{N}\) es un vector normal hacia afuera de \(S\), donde \(S\) es la superficie de la esfera \(x^2 + y^2 + z^2 = 1\).

305. Calcula \(\displaystyle \iint_S \mathbf{F} \cdot \mathbf{N} \, dS\), donde \(\mathbf{F}(x, y, z) = xyz\mathbf{i} + xyz\mathbf{j} + xyz\mathbf{k}\) y \(\mathbf{N}\) es un vector normal hacia afuera de \(S\), donde \(S\) es la superficie de las cinco caras del cubo unitario \(0 \leq x \leq 1, 0 \leq y \leq 1, 0 \leq z \leq 1\) sin la cara \(z = 0\).

Para los siguientes ejercicios, expresa la integral de superficie como una integral doble iterada usando una proyección de \( S \) en el plano \( yz \).

306. \(\displaystyle \iint_{S} xy^2 z^3 \, dS\); \( S \) es la porción en el primer octante del plano \( 2x + 3y + 4z = 12 \).

307. \(\displaystyle \iint_{S} (x^2 – 2y + z) \, dS\); \( S \) es la porción de la gráfica de \( 4x + y = 8 \) limitada por los planos coordenados y el plano \( z = 6 \).

Para los siguientes ejercicios, exprese la integral de superficie como una integral doble iterada usando una proyección de \(S\) en el plano xz:

308. \(\displaystyle \iint_S xy^2 z^3 \, dS\); \(S\) es la porción del primer octante del plano \(2x + 3y + 4z = 12\).

309. \(\displaystyle \iint_S (x^2 – 2y + z) \, dS\); \(S\) es la porción de la gráfica de \(4x + y = 8\) acotada por los planos coordenados y el plano \(z = 6\).

310. Evalúe la integral de superficie \(\displaystyle \iint_S yz \, dS\), donde \(S\) es la parte del primer octante del plano \(x + y + z = \lambda\), donde \(\lambda\) es una constante positiva.

311. Evalúe la integral de superficie \(\displaystyle \iint_S (x^2 z + y^2 z) \, dS\), donde \(S\) es el hemisferio \(x^2 + y^2 + z^2 = a^2\), \(z \geq 0\).

312. Evalúe la integral de superficie \(\displaystyle \iint_S z \, dA\), donde \(S\) es la superficie \(z = \sqrt{x^2 + y^2}\), \(0 \leq z \leq 2\).

313. Evalúe la integral de superficie \(\displaystyle \iint_S x^2 yz \, dS\), donde \(S\) es la parte del plano \(z = 1 + 2x + 3y\) que se encuentra sobre el rectángulo \(0 \leq x \leq 3\) y \(0 \leq y \leq 2\).

314. Evalúe la integral de superficie \(\displaystyle \iint_S yz \, dS\), donde \(S\) es el plano \(x + y + z = 1\) que se encuentra en el primer octante.

315. Evalúe la integral de superficie \(\displaystyle \iint_S yz \, dS\), donde \(S\) es la parte del plano \(z = y + 3\) que se encuentra dentro del cilindro \(x^2 + y^2 = 1\).

Para los siguientes ejercicios, use razonamiento geométrico para evaluar las integrales de superficie dadas.

316. \(\displaystyle \iint_S \sqrt{x^2 + y^2 + z^2} \, dS\), donde \(S\) es la superficie \(x^2 + y^2 + z^2 = 4\), \(z \geq 0\)

317. \(\displaystyle \iint_S (x\mathbf{i} + y\mathbf{j}) \cdot d\mathbf{S}\), donde \(S\) es la superficie \(x^2 + y^2 = 4\), \(1 \leq z \leq 3\), orientada con vectores normales unitarios apuntando hacia afuera

318. \(\displaystyle \iint_S (z\mathbf{k}) \cdot d\mathbf{S}\), donde \(S\) es el disco \(x^2 + y^2 \leq 9\) sobre el plano \(z = 4\), orientado con vectores normales unitarios apuntando hacia arriba

319. Una lámina tiene la forma de una porción de esfera \(x^2 + y^2 + z^2 = a^2\) que se encuentra dentro del cono \(z = \sqrt{x^2 + y^2}\).

Sea S la cáscara esférica centrada en el origen con radio a, y sea C el cono circular recto con un vértice en el origen y un eje de simetría que coincide con el eje z. Determine la masa de la lámina si \(\rho(x, y, z) = x^2 y^2 z\).

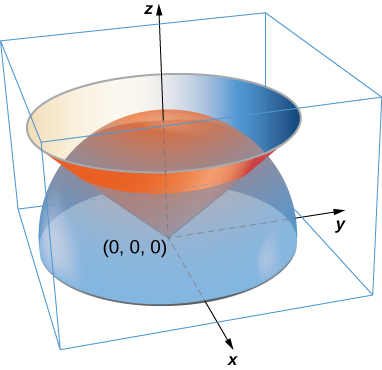
320. Una lámina tiene la forma de una porción de esfera \(x^2 + y^2 + z^2 = a^2\) que se encuentra dentro del cono \(z = \cot \phi_0 \sqrt{x^2 + y^2}\).

Sea S la cáscara esférica centrada en el origen con radio a, y sea C el cono circular recto con un vértice en el origen y un eje de simetría que coincide con el eje z. Suponga que el ángulo entre los lados del cono y el eje z es \(\phi_0\), con \(0 \leq \phi_0 < \frac{\pi}{2}\). Determine la masa de esa porción de la forma encerrada en la intersección de S y C. Asuma \(\rho(x, y, z) = x^2 y^2 z\).

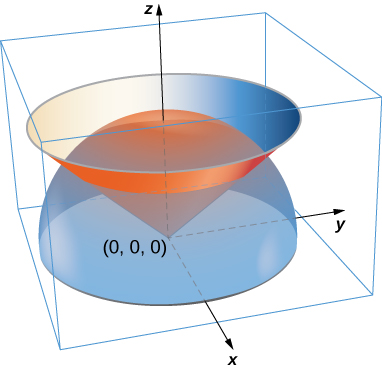
321. Un vaso de papel tiene la forma de un cono circular recto invertido de altura 6 pulgadas y radio superior de 3 pulgadas. Si el vaso está lleno de agua que pesa 62.5 lb/ft³, encuentre la fuerza total ejercida por el agua sobre la superficie interior del vaso.

Para los siguientes ejercicios, el campo vectorial de flujo de calor para objetos conductores es \(\mathbf{F} = -k \nabla T\), donde \(T(x, y, z)\) es la temperatura en el objeto y \(k > 0\) es una constante que depende del material. Encuentre el flujo hacia afuera de \(\mathbf{F}\) a través de las siguientes superficies \(S\) para las distribuciones de temperatura dadas y asuma \(k = 1\).

322. \(T(x, y, z) = 100e^{-x – y}\); \(S\) consiste en las caras del cubo \(|x| \leq 1\), \(|y| \leq 1\), \(|z| \leq 1\).

323. \(T(x, y, z) = -\ln(x^2 + y^2 + z^2)\); \(S\) es la esfera \(x^2 + y^2 + z^2 = a^2\).

Para los siguientes ejercicios, considere los campos radiales \(\mathbf{F} = \frac{\langle x, y, z \rangle}{(x^2 + y^2 + z^2)^{p/2}} = \frac{\mathbf{r}}{||\mathbf{r}||^p}\) donde \(p\) es un número real. Sea \(S\) consistente en las esferas \(A\) y \(B\) centradas en el origen con radios \(0 < a < b\). El flujo total hacia afuera a través de \(S\) consiste en el flujo hacia afuera a través de la esfera exterior \(B\) menos el flujo hacia adentro de \(S\) a través de la esfera interior \(A\).

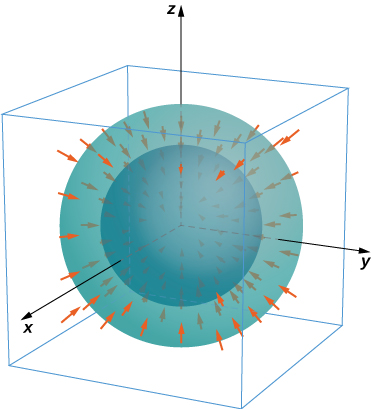
324. Encuentre el flujo total a través de \(S\) con \(p = 0\).

325. Demuestre que para \(p = 3\) el flujo a través de \(S\) es independiente de \(a\) y \(b\).