| 10.14 Campos de vectores conservadores |

Ejercicios propuestos para el Capítulo 10.14

99. ¿Verdadero o falso? Si un campo vectorial \( \mathbf{F} \) es conservativo en una región abierta y conexa \( D \), entonces las integrales de línea de \( \mathbf{F} \) son independientes de la trayectoria en \( D \), independientemente de la forma de \( D \).

100. ¿Verdadero o falso? La función \( \mathbf{r}(t) = \mathbf{a} + t \, (\mathbf{b} – \mathbf{a}) \), donde \( 0 \leq t \leq 1 \), parametriza el segmento de línea recta desde \( \mathbf{a} \) hasta \( \mathbf{b} \).

101. ¿Verdadero o falso? El campo vectorial \( \mathbf{F}(x, y, z) = (y \sin z) \mathbf{i} + (x \sin z) \mathbf{j} + (xy \cos z) \mathbf{k} \) es conservativo.

102. ¿Verdadero o falso? El campo vectorial \( \mathbf{F}(x, y, z) = y \mathbf{i} + (x + z) \mathbf{j} – y \mathbf{k} \) es conservativo.

103. Verifica el Teorema Fundamental para Integrales de Línea para \( \int_C \mathbf{F} \cdot d\mathbf{r} \) calculando la integral usando una parametrización y, por separado, encontrando una función potencial para el caso cuando \( \mathbf{F}(x, y) = (2x + 2y) \mathbf{i} + (2x + 2y) \mathbf{j} \) y \( C \) es una porción del círculo orientado positivamente \( x^2 + y^2 = 25 \) desde \((5, 0)\) hasta \((3, 4)\).

104. [T] Encuentra \( \int_C \mathbf{F} \cdot d\mathbf{r} \), donde \( \mathbf{F}(x, y) = (y e^{xy} + \cos x) \mathbf{i} + \left( x e^{xy} + \frac{1}{y^{2}+1} \right) \mathbf{j} \) y \( C \) es una porción de la curva \( y = \sin x \) desde \( x = 0 \) hasta \( x = \frac{\pi}{2} \).

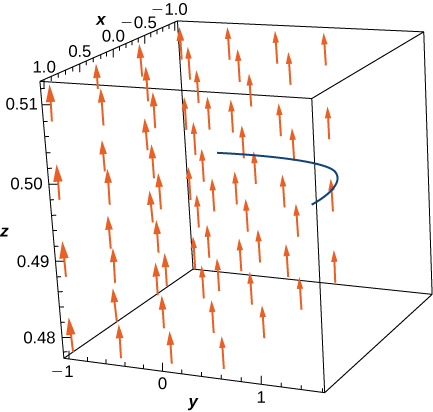
105. [T] Evalúa la integral de línea \( \int_C \mathbf{F} \cdot d\mathbf{r} \), donde \( \mathbf{F}(x, y) = (e^x \sin y – y) \mathbf{i} + (e^x \cos y – x – 2) \mathbf{j} \), y \( C \) es la trayectoria dada por \( \mathbf{r}(t) = \left[ t^3 \sin \frac{\pi t}{2} \right] \mathbf{i} – \left[ \frac{\pi}{2} \cos \left( \frac{\pi t}{2} + \frac{\pi}{2} \right) \right] \mathbf{j} \) para \( 0 \leq t \leq 1 \).

Para los siguientes ejercicios, determina si el campo vectorial es conservativo y, si lo es, encuentra la función potencial.

106. \(\mathbf{F}(x, y) = 2xy^3\mathbf{i} + 3y^2x^2\mathbf{j}\)

107. \(\mathbf{F}(x, y) = (-y + e^x\sin y)\mathbf{i} + [(x+2)e^x\cos y]\mathbf{j}\)

108. \(\mathbf{F}(x, y) = (e^{2x}\sin y)\mathbf{i} + [e^{2x}\cos y]\mathbf{j}\)

109. \(\mathbf{F}(x, y) = (6x + 5y)\mathbf{i} + (5x + 4y)\mathbf{j}\)

110. \(\mathbf{F}(x, y) = [2x\cos(y) – y\cos(x)]\mathbf{i} + [-x^2\sin(y) – \sin(x)]\mathbf{j}\)

111. \(\mathbf{F}(x, y) = [ye^x + \sin(y)]\mathbf{i} + [e^x + x\cos(y)]\mathbf{j}\)

Para los siguientes ejercicios, evalúa las integrales de línea utilizando el Teorema Fundamental de las Integrales de Línea.

112. \(\int_C (y\mathbf{i} + x\mathbf{j}) \cdot d\mathbf{r}\), donde \( C \) es cualquier camino de \( (0, 0) \) a \( (2, 4) \).

113. \(\int_C (2y \, dx + 2x \, dy)\), donde \( C \) es el segmento de recta de \( (0, 0) \) a \( (4, 4) \).

114. \(\int_C \left[ \arctan \frac{y}{x} – \frac{xy}{x^2 + y^2} \right] dx + \left[ \frac{x^2}{x^2 + y^2} + e^{-y}(1 – y) \right] dy\), donde \( C \) es cualquier curva suave de \( (1, 1) \) a \( (-1, 2) \).

115. Hallar el campo vectorial conservador para la función potencial

\[ f(x, y) = 5x^2 + 3xy + 10y^2. \]

Para los siguientes ejercicios, determine si el campo vectorial es conservativo y, de ser así, encuentre una función potencial.

116. \( \mathbf{F}(x, y) = (12xy) \mathbf{i} + 6 \left( x^2 + y^2 \right) \mathbf{j} \)

117. \( \mathbf{F}(x, y) = (e^x \cos y) \mathbf{i} + 6 \left( e^x \sin y \right) \mathbf{j} \)

118. \( \mathbf{F}(x, y) = \left( 2xy e^{x^2y} \right) \mathbf{i} + \left( x^2 e^{x^2y} \right) \mathbf{j} \)

119. \( \mathbf{F}(x, y, z) = (ye^z) \mathbf{i} + (xe^z) \mathbf{j} + (xy e^z) \mathbf{k} \)

120. \( \mathbf{F}(x, y, z) = (\sin y) \mathbf{i} – (x \cos y) \mathbf{j} + \mathbf{k} \)

121. \( \mathbf{F}(x, y, z) = \left( -\frac{1}{y} \right) \mathbf{i} + \left( \frac{x}{y^2} \right) \mathbf{j} + (2z – 1) \mathbf{k} \)

122. \( \mathbf{F}(x, y, z) = 3z^2 \mathbf{i} – \cos y \mathbf{j} + 2xz \mathbf{k} \)

123. \( \mathbf{F}(x, y, z) = (2xy) \mathbf{i} + \left( x^2 + 2yz \right) \mathbf{j} + y^2 \mathbf{k} \)

124. \( \mathbf{F}(x, y) = (e^x \cos y) \mathbf{i} + 6 \left( e^x \sin y \right) \mathbf{j} \)

125. \( \mathbf{F}(x, y) = \left( 2xy e^{x^2y} \right) \mathbf{i} + \left( x^2 e^{x^2y} \right) \mathbf{j} \)

Para los siguientes ejercicios, evalúa la integral usando el Teorema Fundamental de las Integrales de Línea.

126. Evaluar \[ \int_C \nabla f \cdot d\mathbf{r}, \] donde \( f(x, y, z) = \cos(\pi x) + \sin(\pi y) – \pi y \) y \( C \) es cualquier camino que comience en \( (1, \frac{1}{2}, 2) \) y termine en \( (2, 1, -1) \).

127. [T] Evaluar \[ \int_C \nabla f \cdot d\mathbf{r}, \] donde \( f(x, y) = xy + e^x \) y \( C \) es una línea recta desde \( (0, 0) \) hasta \( (2, 1) \).

128. [T] Evaluar \[ \int_C \nabla f \cdot d\mathbf{r}, \] donde \( f(x, y) = x^2 y – x \) y \( C \) es cualquier camino en un plano desde \( (1, 2) \) hasta \( (3, 2) \).

129. Evaluar \[ \int_C \nabla f \cdot d\mathbf{r}, \] donde \( f(x, y, z) = xyz^2 – yz \) y \( C \) tiene punto inicial \( (1, 2, 3) \) y punto terminal \( (3, 5, 1) \).

Para los siguientes ejercicios, sean \( \mathbf{F}(x, y) = 2xy^2\mathbf{i} + (2yx^2 + 2y)\mathbf{j} \), \( \mathbf{G}(x, y) = (y + x)\mathbf{i} + (y – x)\mathbf{j} \), y que \( C_1 \) sea la curva formada por el círculo de radio 2, centrado en el origen y orientado en sentido contrario a las agujas del reloj, y \( C_2 \) sea la curva que consta de un segmento de recta de \( (0, 0) \) a \( (1, 1) \) seguido de un segmento de recta de \( (1, 1) \) a \( (3, 1) \).

\[ \mathbf{F}(x, y) = 2xy^{2}\mathbf{i} + (2yx^{2} + 2y)\mathbf{j} \]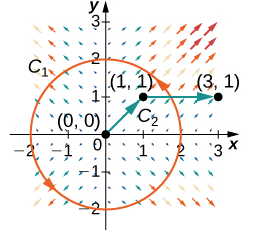

\[ \mathbf{G}(x, y) = (y + x)\mathbf{i} + (y – x)\mathbf{j} \]

130. Calcula la integral de línea de \( \mathbf{F} \) sobre \( C_1 \).

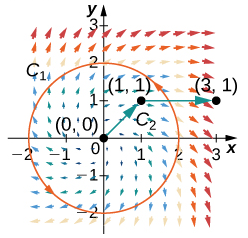
131. Calcula la integral de línea de \( \mathbf{G} \) sobre \( C_1 \).

132. Calcula la integral de línea de \( \mathbf{F} \) sobre \( C_2 \).

133. Calcula la integral de línea de \( \mathbf{G} \) sobre \( C_2 \).

134. [T] Sea \( \mathbf{F}(x, y, z) = x^2 \mathbf{i} + z \sin(yz) \mathbf{j} + y \sin(yz) \mathbf{k} \). Calcula \( \int_C \mathbf{F} \cdot d\mathbf{r} \), donde \( C \) es una trayectoria desde

\[ A = (0, 0, 1) \text{ hasta } B = (3, 1, 2). \]

135. [T] Encuentra la integral de línea \( \int_C \mathbf{F} \cdot d\mathbf{r} \) del campo vectorial \( \mathbf{F}(x, y, z) = 3x^2 z \mathbf{i} + z^2 \mathbf{j} + (x^3 + 2yz) \mathbf{k} \) a lo largo de la curva \( C \) parametrizada por

\[ \mathbf{r}(t) = \left( \frac{\ln t}{\ln 2} \right) \mathbf{i} + \frac{t^3}{2} \mathbf{j} + t \cos(\pi t) \mathbf{k}, \quad 1 \leq t \leq 4. \]

Para los siguientes ejercicios, muestra que los siguientes campos vectoriales son conservativos utilizando una computadora. Calcula \(\int_{C}\mathbf{F}\cdot d\mathbf{r}\) para la curva dada.

136. \(\mathbf{F} = \left(xy^{2} + 3x^{2}y\right)\mathbf{i} + \left(x + y\right)x^{2}\mathbf{j}\); \(C\) es la curva que consiste en segmentos de línea desde \((1, 1)\) hasta \((0, 2)\) y luego hasta \((3, 0)\).

137. \(\mathbf{F} = \frac{2x}{y^{2} + 1}\mathbf{i} – \frac{2y\left(x^{2} + 1\right)}{\left(y^{2} + 1\right)^{2}}\mathbf{j}\); \(C\) está parametrizada por \(x = t^{3} – 1\), \(y = t^{6} – t\), \(0 \leq t \leq 1\).

138. [T] \(\mathbf{F} = \left[\cos\left(xy^{2}\right) – xy^{2}\sin\left(xy^{2}\right)\right]\mathbf{i} – 2x^{2}y\sin\left(xy^{2}\right)\mathbf{j}\); \(C\) es la curva \(\left(e^{t}, e^{t+1}\right)\), \(-1 \leq t \leq 0\).

139. La masa de la Tierra es aproximadamente \(6 \times 10^{27}\) g y la del Sol es 330,000 veces mayor. La constante gravitacional es \(6.7 \times 10^{-8}\) cm\(^3\)/s\(^2\)·g. La distancia de la Tierra al Sol es aproximadamente \(1.5 \times 10^{12}\) cm. Calcula, aproximadamente, el trabajo necesario para aumentar la distancia de la Tierra al Sol en 1 cm.

140. [T] Sea \(\mathbf{F}(x, y, z) = \left(e^{x}\sin y\right)\mathbf{i} + \left(e^{x}\cos y\right)\mathbf{j} + z^{2}\mathbf{k}\). Evalúa la integral \(\int_{C}\mathbf{F}\cdot ds\), donde \(C\) es la curva \(\left(\sqrt{t}, t^{3}, e^{\sqrt{t}}\right)\), \(0 \leq t \leq 1\).

141. [T] Sea \(\mathbf{c}:[1, 2] \rightarrow \mathbb{R}^{2}\) dada por \(x = e^{t-1}\), \(y = \sin\left(\frac{\pi}{t}\right)\). Usa una computadora para calcular la integral \(\int_{C}\mathbf{F}\cdot ds = \int_{C}2x\,\cos y\,dx – x^{2}\sin y\,dy\), donde \(\mathbf{F} = \left(2x\,\cos y\right)\mathbf{i} – \left(x^{2}\sin y\right)\mathbf{j}\).

142. [T] Usa un sistema de álgebra computacional para encontrar la masa de un cable que yace a lo largo de la curva \(\mathbf{r}(t) = \left(t^{2} – 1\right)\mathbf{j} + 2t\mathbf{k}\), \(0 \leq t \leq 1\), si la densidad es \(\frac{3}{2}t\).

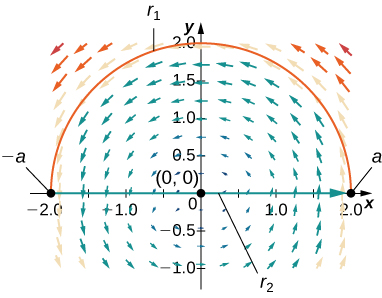
143. Encuentra la circulación y el flujo del campo \(\mathbf{F} = -y\mathbf{i} + x\mathbf{j}\) alrededor y a través de la trayectoria semicircular cerrada que consiste en el arco semicircular \(\mathbf{r}_{1}(t) = \left(a\cos t\right)\mathbf{i} + \left(a\sin t\right)\mathbf{j}\), \(0 \leq t \leq \pi\), seguido por el segmento de línea \(\mathbf{r}_{2}(t) = t\mathbf{i}\), \(-a \leq t \leq a\).

144. Calcula \[ \int_C \cos x \, \cos y \, dx – \sin x \, \sin y \, dy, \] donde \( c(t) = (t, t^2) \), \( 0 \leq t \leq 1 \).

145. Completa la prueba del Test de Independencia de la Trayectoria para Campos Conservativos mostrando que

\[ f_y = Q(x, y). \]