| 11. Diferenciación de funciones de varias variables | Ejercicios propuestos para el Capítulo 11.8 |
11.8 Multiplicadores de Lagrange
Objetivos de aprendizaje
- 11.8.1 Utilizar el método de los multiplicadores de Lagrange para resolver problemas de optimización con una restricción.
- 11.8.2 Utilizar el método de los multiplicadores de Lagrange para resolver problemas de optimización con dos restricciones.
Resolver problemas de optimización para funciones de dos o más variables puede ser similar a resolver este tipo de problemas en el cálculo de una variable. Sin embargo, las técnicas para tratar con varias variables nos permiten resolver problemas de optimización más variados, en los cuales es necesario considerar condiciones adicionales o restricciones. En esta sección, examinamos uno de los métodos más comunes y útiles para resolver problemas de optimización con restricciones.
Multiplicadores de Lagrange
El Ejemplo 11.7.4 fue una situación aplicada que implicaba maximizar una función de beneficio, sujeta a ciertas restricciones. En ese ejemplo, las restricciones involucraban un número máximo de pelotas de golf que podían producirse y venderse en 1 mes \( (x) \), y un número máximo de horas de publicidad que podían comprarse por mes \( (y) \).
Supongamos que estas se combinaron en una restricción presupuestaria, como \( 20x + 4y \leq 216 \), que tuvo en cuenta el costo de producir las pelotas de golf y el número de horas de publicidad compradas por mes. El objetivo sigue siendo maximizar el beneficio, pero ahora existe un tipo diferente de restricción sobre los valores de \( x \) e \( y \).
Esta restricción, cuando se combina con la función de beneficio \[ f(x, y) = 48x + 96y – x^2 – 2xy – 9y^2 \] es un ejemplo de un problema de optimización, y la función \( f(x, y) \) se denomina función objetivo. A continuación se presenta un gráfico de varias curvas de nivel de la función \( f(x, y) \).
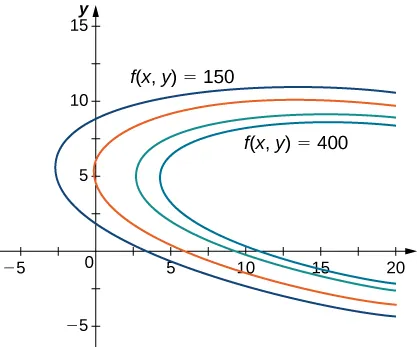
Figura 11.8.1 Gráfica de las curvas de nivel de la función \( f(x,y) = 48x + 96y – x^2 – 2xy – 9y^2 \), correspondientes a \( c = 150, 250, 350 \) y \( 400 \).
En la Figura 11.8.1, el valor de \(c\) representa distintos niveles de ganancia (es decir, valores de la función \(f\)). A medida que el valor de \(c\) aumenta, la curva se desplaza hacia la derecha. Dado que nuestro objetivo es maximizar la ganancia, queremos elegir una curva lo más a la derecha posible.
Si no existiera ninguna restricción sobre la cantidad de pelotas de golf que la empresa puede producir, ni sobre el número de unidades de publicidad disponibles, entonces podríamos producir tantas pelotas de golf como quisiéramos y anunciar tanto como deseáramos, y no existiría una ganancia máxima para la empresa.
Desafortunadamente, tenemos una restricción presupuestaria que se modela mediante la desigualdad \( 20x + 4y \leq 216 \). Para ver cómo esta restricción interactúa con la función de ganancia, la Figura 11.8.2 muestra la gráfica de la recta \( 20x + 4y = 216 \) superpuesta sobre la gráfica anterior.
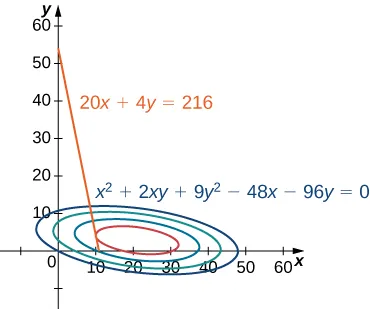
Figura 11.8.2 Gráfica de las curvas de nivel de la función \( f(x,y) = 48x + 96y – x^2 – 2xy – 9y^2 \), correspondientes a \( c = 150, 250, 350 \) y \( 395 \). La gráfica en rojo corresponde a la función de restricción.
Como se mencionó anteriormente, la ganancia máxima ocurre cuando la curva de nivel está lo más a la derecha posible. Sin embargo, el nivel de producción correspondiente a esta ganancia máxima también debe satisfacer la restricción presupuestaria, por lo que el punto en el que ocurre dicha ganancia debe estar también sobre (o a la izquierda de) la línea roja en la Figura 11.8.2. La inspección de esta gráfica revela que este punto existe donde la recta es tangente a la curva de nivel de f.
El método de prueba y error muestra que este nivel de ganancia parece estar alrededor de 395, cuando x y y son ambos apenas menores que 5. Retomaremos la solución de este problema más adelante en esta sección. Desde un punto de vista teórico, en el punto donde la curva de ganancia es tangente a la recta de restricción, el gradiente de ambas funciones evaluadas en ese punto debe apuntar en la misma (o en la dirección opuesta). Recuerde que el gradiente de una función de más de una variable es un vector. Si dos vectores apuntan en la misma (o en direcciones opuestas), entonces uno debe ser un múltiplo constante del otro. Esta idea es la base del método de los multiplicadores de Lagrange.
Teorema 11.8.1. Método de los multiplicadores de Lagrange: una restricción
Sean \(f\) y \(g\) funciones de dos variables con derivadas parciales continuas en cada punto de algún conjunto abierto que contiene a la curva suave \(g(x, y) = 0\). Suponga que \(f\), cuando se restringe a puntos en la curva \(g(x, y) = 0\), tiene un extremo local en el punto \((x_0, y_0)\) y que \(\nabla g(x_0, y_0) \neq 0\). Entonces existe un número \(\lambda\) llamado multiplicador de Lagrange, para el cual
$$\nabla f(x_0, y_0) = \lambda \nabla g(x_0, y_0).$$
♦
Demostración:
Supongamos que un extremo restringido ocurre en el punto \((x_0, y_0)\). Además, asumimos que la ecuación \(g(x,y) = 0\) puede parametrizarse suavemente como:
\(x = x(s)\) y \(y = y(s)\)
donde \(s\) es un parámetro de longitud de arco con punto de referencia \((x_0, y_0)\) en \(s = 0\). Por lo tanto, la cantidad \(z = f(x(s), y(s))\) tiene un máximo relativo o un mínimo relativo en \(s = 0\), lo que implica que \(\frac{dz}{ds} = 0\) en ese punto. A partir de la regla de la cadena:
$$\frac{dz}{ds} = \frac{\partial f}{\partial x} \cdot \frac{dx}{ds} + \frac{\partial f}{\partial y} \cdot \frac{dy}{ds} = \left( \frac{\partial f}{\partial x}\mathbf{i} + \frac{\partial f}{\partial y}\mathbf{j} \right) \cdot \left( \frac{dx}{ds}\mathbf{i} + \frac{dy}{ds}\mathbf{j} \right) = 0$$
donde las derivadas se evalúan en \(s = 0\). Sin embargo, el primer factor en el producto punto es el gradiente de \(f\), y el segundo factor es el vector tangente unitario \(\mathbf{T}(0)\) a la curva de restricción. Dado que el punto \((x_0, y_0)\) corresponde a \(s = 0\), de esta ecuación se deduce que:
$$\nabla f(x_0, y_0) \cdot \mathbf{T}(0) = 0$$
lo que implica que el gradiente es \(\mathbf{0}\) o es normal a la curva de restricción en un extremo relativo restringido. No obstante, la curva de restricción \(g(x,y) = 0\) es una curva de nivel para la función \(g(x,y)\), de modo que si \(\nabla g(x_0, y_0) \neq \mathbf{0}\), entonces \(\nabla g(x_0, y_0)\) es normal a esta curva en \((x_0, y_0)\). Se sigue, entonces, que existe algún escalar \(\lambda\) tal que:
$$\nabla f(x_0, y_0) = \lambda \nabla g(x_0, y_0)$$
♦
Para aplicar el Método de los multiplicadores de Lagrange: una restricción a un problema de optimización similar al del fabricante de pelotas de golf, necesitamos una estrategia para la resolución del problema.
Estrategia de resolución de problemas. Pasos para usar los multiplicadores de Lagrange
Pasos para resolver problemas de optimización restringida
- Determine la función objetivo \( f(x, y) \) y la función de restricción \( g(x, y) \). ¿El problema requiere maximizar o minimizar la función objetivo?
- Configure un sistema de ecuaciones utilizando la siguiente plantilla:
$$\begin{cases} \nabla f(x_0, y_0) &= \lambda \nabla g(x_0, y_0) \\ g(x_0, y_0) &= 0 \end{cases}$$
- Resuelva el sistema para hallar \( x_0 \) y \( y_0 \).
- El mayor de los valores de \( f \) en las soluciones encontradas en el paso 3 maximiza a \( f \); el menor de esos valores minimiza a \( f \).
♦
Ejemplo ilustrativo 11.8.1. Uso de los multiplicadores de Lagrange
Utilice el método de los multiplicadores de Lagrange para encontrar el valor mínimo de la función \( f(x,y) = x^2 + 4y^2 – 2x + 8y \), sujeta a la restricción \( x + 2y = 7 \).
Solución:
Sigamos la estrategia de resolución de problemas:
- La función de optimización es \( f(x, y) = x^2 + 4y^2 – 2x + 8y \). Para determinar la función de restricción, primero debemos restar 7 de ambos lados de la restricción. Esto da \( x + 2y – 7 = 0 \). La función de restricción es igual al lado izquierdo, por lo que \( g(x, y) = x + 2y – 7 \). El problema nos pide hallar el valor mínimo de \( f \), sujeto a la restricción.
-
Luego, debemos calcular los gradientes de tanto \( f \) como \( g \):
$$\nabla f(x, y) = (2x – 2)\mathbf{i} + (8y + 8)\mathbf{j}$$ $$\nabla g(x, y) = \mathbf{i} + 2\mathbf{j}$$
La ecuación \( \nabla f(x_0, y_0) = \lambda \nabla g(x_0, y_0) \) se convierte en:$$(2x_0 – 2)\mathbf{i} + (8y_0 + 8)\mathbf{j} = \lambda(\mathbf{i} + 2\mathbf{j}),$$
que puede reescribirse como:$$(2x_0 – 2)\mathbf{i} + (8y_0 + 8)\mathbf{j} = \lambda\mathbf{i} + 2\lambda\mathbf{j}.$$
A continuación, igualamos los coeficientes de \( \mathbf{i} \) y \( \mathbf{j} \):$$2x_0 – 2 = \lambda$$ $$8y_0 + 8 = 2\lambda$$
La ecuación \( g(x_0, y_0) = 0 \) se convierte en \( x_0 + 2y_0 – 7 = 0 \). Por lo tanto, el sistema de ecuaciones que necesita ser resuelto es:$$\begin{cases} 2x_0 – 2 &= \lambda \\ 8y_0 + 8 &= 2\lambda \\ x_0 + 2y_0 – 7 &= 0 \end{cases}$$
-
Este es un sistema lineal de tres ecuaciones con tres variables. Comenzamos resolviendo la segunda ecuación para \( \lambda \) y sustituyéndola en la primera ecuación. Esto da \( \lambda = 4y_0 + 4 \), por lo que al sustituir esto en la primera ecuación obtenemos:
$$2x_0 – 2 = 4y_0 + 4$$
Resolviendo esta ecuación para \( x_0 \) obtenemos \( x_0 = 2y_0 + 3 \). Luego sustituimos esto en la tercera ecuación:$$(2y_0 + 3) + 2y_0 – 7 = 0$$ $$4y_0 – 4 = 0$$ $$y_0 = 1$$
Dado que \( x_0 = 2y_0 + 3 \), esto nos da \( x_0 = 5 \). -
A continuación, sustituimos \( (5, 1) \) en \( f(x, y) = x^2 + 4y^2 – 2x + 8y \), lo que da:
$$f(5, 1) = 5^2 + 4(1)^2 – 2(5) + 8(1) = 27$$
Para asegurar que esto corresponde a un valor mínimo en la función de restricción, probemos algunos otros valores, como las intersecciones de \( g(x, y) = 0 \), que son \( (7, 0) \) y \( (0, 3.5) \). Obtenemos \( f(7, 0) = 35 \) y \( f(0, 3.5) = 77 \), por lo que parece que \( f \) tiene un mínimo en \( (5, 1) \).
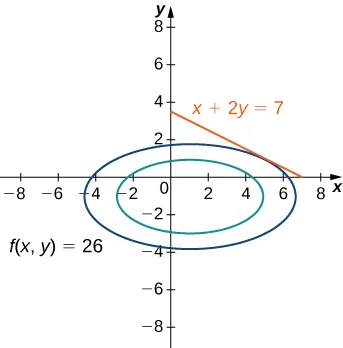
Figura 11.8.3 Gráfica de las curvas de nivel de la función \( f(x,y) = x^2 + 4y^2 – 2x + 8y \), correspondientes a \( c = 10 \) y \( 26 \). La gráfica en rojo corresponde a la función de restricción.
♦
Ejercicio de control 11.8.1
Utilice el método de los multiplicadores de Lagrange para encontrar el valor máximo de la función \( f(x,y) = 9x^2 + 36xy – 4y^2 – 18x – 8y \), sujeta a la restricción \( 3x + 4y = 32 \). ♦
Ahora regresemos al problema planteado al comienzo de la sección.
Ejemplo ilustrativo 11.8.2. Pelotas de golf y multiplicadores de Lagrange
El fabricante de pelotas de golf, Pro-T, ha desarrollado un modelo de ganancia que depende del número \( x \) de pelotas de golf vendidas por mes (medido en miles) y del número de horas mensuales de publicidad \( y \), de acuerdo con la función
\( z = f(x,y) = 48x + 96y – x^2 – 2xy – 9y^2, \)
donde \( z \) se mide en miles de dólares. La función de restricción presupuestaria que relaciona el costo de la producción de miles de pelotas de golf y las unidades de publicidad está dada por
\( 20x + 4y = 216. \)
Halle los valores de \( x \) y \( y \) que maximizan la ganancia y determine la ganancia máxima.
Solución:
Nuevamente, sigamos la estrategia de resolución de problemas:
- La función de optimización es \( f(x, y) = 48x + 96y – x^2 – 2xy – 9y^2 \). Para determinar la función de restricción, primero restamos 216 de ambos lados de la restricción y luego dividimos ambos lados por 4, lo que nos da \( 5x + y – 54 = 0 \). La función de restricción es igual al lado izquierdo, por lo tanto \( g(x, y) = 5x + y – 54 \). El problema nos pide resolver para el valor máximo de \( f \), sujeto a esta restricción.
-
Por lo tanto, calculamos los gradientes de tanto \( f \) como \( g \):
$$\nabla f(x, y) = (48 – 2x – 2y)\mathbf{i} + (96 – 2x – 18y)\mathbf{j}$$ $$\nabla g(x, y) = 5\mathbf{i} + \mathbf{j}$$
La ecuación \( \nabla f(x_0, y_0) = \lambda \nabla g(x_0, y_0) \) se convierte en:$$(48 – 2x_0 – 2y_0)\mathbf{i} + (96 – 2x_0 – 18y_0)\mathbf{j} = \lambda(5\mathbf{i} + \mathbf{j}),$$
que puede reescribirse como:$$(48 – 2x_0 – 2y_0)\mathbf{i} + (96 – 2x_0 – 18y_0)\mathbf{j} = 5\lambda\mathbf{i} + \lambda\mathbf{j}.$$
Luego, igualamos los coeficientes de \( \mathbf{i} \) y \( \mathbf{j} \):$$48 – 2x_0 – 2y_0 = 5\lambda$$ $$96 – 2x_0 – 18y_0 = \lambda$$
La ecuación \( g(x_0, y_0) = 0 \) se convierte en \( 5x_0 + y_0 – 54 = 0 \). Por lo tanto, el sistema de ecuaciones que debe resolverse es:$$\begin{cases} 48 – 2x_0 – 2y_0 &= 5\lambda \\ 96 – 2x_0 – 18y_0 &= \lambda \\ 5x_0 + y_0 – 54 &= 0 \end{cases}$$
-
Usamos el lado izquierdo de la segunda ecuación para sustituir \( \lambda \) en la primera ecuación:
$$48 – 2x_0 – 2y_0 = 5(96 – 2x_0 – 18y_0)$$ $$48 – 2x_0 – 2y_0 = 480 – 10x_0 – 90y_0$$ $$8x_0 = 432 – 88y_0$$ $$x_0 = 54 – 11y_0$$
Luego sustituimos esto en la tercera ecuación:$$5(54 – 11y_0) + y_0 – 54 = 0$$ $$270 – 55y_0 + y_0 – 54 = 0$$ $$216 – 54y_0 = 0$$ $$y_0 = 4$$
Dado que \( x_0 = 54 – 11y_0 \), esto nos da \( x_0 = 10 \). -
A continuación, sustituimos \( (10, 4) \) en \( f(x, y) = 48x + 96y – x^2 – 2xy – 9y^2 \), lo que da:
$$f(10, 4) = 48(10) + 96(4) – (10)^2 – 2(10)(4) – 9(4)^2$$ $$f(10, 4) = 480 + 384 – 100 – 80 – 144 = 540$$
Por lo tanto, el beneficio máximo que se puede alcanzar, sujeto a las restricciones presupuestarias, es de $540,000 con un nivel de producción de 10,000 pelotas de golf y 4 horas de publicidad compradas al mes. Verifiquemos para asegurarnos de que esto es realmente un máximo. Los puntos extremos de la línea que define la restricción son \( (10.8, 0) \) y \( (0, 54) \). Evaluemos \( f \) en ambos puntos:$$f(10.8, 0) = 48(10.8) + 96(0) – 10.8^2 – 2(10.8)(0) – 9(0^2) = 401.76$$ $$f(0, 54) = 48(0) + 96(54) – 0^2 – 2(0)(54) – 9(54^2) = -21,060$$
El segundo valor representa una pérdida, ya que no se producen pelotas de golf. Ninguno de estos valores supera 540, por lo que parece que nuestro extremo es un valor máximo de \( f \).
Ejercicio de control 11.8.2
Una empresa ha determinado que su nivel de producción está dado por la función de Cobb-Douglas \( f(x,y) = 2.5x^{0.45}y^{0.55} \), donde \( x \) representa el número total de horas de trabajo en un año y \( y \) representa el total de capital invertido por la empresa.
Suponga que una unidad de trabajo cuesta \( \$40 \) y una unidad de capital cuesta \( \$50 \).
Utilice el método de los multiplicadores de Lagrange para encontrar el valor máximo de \( f(x,y) = 2.5x^{0.45}y^{0.55} \), sujeto a una restricción presupuestaria de \( \$500{,}000 \) por año. ♦
En el caso de una función de optimización con tres variables y una sola función de restricción, también es posible utilizar el método de los multiplicadores de Lagrange para resolver un problema de optimización.
Un ejemplo de una función de optimización con tres variables podría ser la función de Cobb-Douglas del ejemplo anterior: \( f(x,y,z) = x^{0.2} y^{0.4} z^{0.4} \), donde \( x \) representa el costo de la mano de obra, \( y \) representa el capital invertido y \( z \) representa el costo de la publicidad.
El método es el mismo que para el caso de una función de dos variables; las ecuaciones que deben resolverse son:
\( \nabla f(x,y,z) = \lambda \nabla g(x,y,z) \)
\( g(x,y,z) = 0. \)
Ejemplo ilustrativo 11.8.3. Multiplicadores de Lagrange con una función de optimización de tres variables
Halle el valor mínimo de la función \( f(x,y,z) = x^2 + y^2 + z^2 \), sujeta a la restricción \( x + y + z = 1 \).
Solución:
- La función de optimización es \( f(x, y, z) = x^2 + y^2 + z^2 \). Para determinar la función de restricción, restamos 1 de cada lado de la restricción: \( x + y + z – 1 = 0 \), lo que nos da la función de restricción como \( g(x, y, z) = x + y + z – 1 \).
-
A continuación, calculamos \( \nabla f(x, y, z) \) y \( \nabla g(x, y, z) \):
$$\nabla f(x, y, z) = \langle 2x, 2y, 2z \rangle$$ $$\nabla g(x, y, z) = \langle 1, 1, 1 \rangle$$
Esto nos lleva a las ecuaciones:$$\langle 2x_0, 2y_0, 2z_0 \rangle = \lambda \langle 1, 1, 1 \rangle$$ $$x_0 + y_0 + z_0 – 1 = 0$$
las cuales pueden reescribirse de la siguiente forma:$$\begin{cases} 2x_0 &= \lambda \\ 2y_0 &= \lambda \\ 2z_0 &= \lambda \\ x_0 + y_0 + z_0 – 1 &= 0 \end{cases}$$
- Dado que cada una de las tres primeras ecuaciones tiene a \( \lambda \) en el lado derecho, sabemos que \( 2x_0 = 2y_0 = 2z_0 \) y las tres variables son iguales entre sí. Sustituyendo \( y_0 = x_0 \) y \( z_0 = x_0 \) en la última ecuación se obtiene \( 3x_0 – 1 = 0 \), por lo que \( x_0 = \frac{1}{3} \), \( y_0 = \frac{1}{3} \) y \( z_0 = \frac{1}{3} \), lo cual corresponde a un punto crítico en la curva de restricción.
-
Luego, evaluamos \( f \) en el punto \( \left( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right) \):
$$f\left( \frac{1}{3}, \frac{1}{3}, \frac{1}{3} \right) = \left( \frac{1}{3} \right)^2 + \left( \frac{1}{3} \right)^2 + \left( \frac{1}{3} \right)^2 = \frac{3}{9} = \frac{1}{3}$$
Por lo tanto, un extremo de la función es \( \frac{1}{3} \). Para verificar que es un mínimo, elegimos otros puntos que satisfagan la restricción y calculamos \( f \) en esos puntos. Por ejemplo:$$f(1, 0, 0) = 1^2 + 0^2 + 0^2 = 1$$ $$f(0, -2, 3) = 0^2 + (-2)^2 + 3^2 = 13$$
Ambos valores son mayores que \( \frac{1}{3} \), lo que nos lleva a creer que el extremo es un mínimo. ♦
Ejercicio de control 11.8.3
Utilice el método de los multiplicadores de Lagrange para encontrar el valor mínimo de la función \( f(x,y,z) = x + y + z \), sujeta a la restricción \( x^2 + y^2 + z^2 = 1 \). ♦
Problemas con dos restricciones
El método de los multiplicadores de Lagrange puede aplicarse a problemas con más de una restricción. En este caso, la función de optimización \( w \) es una función de tres variables:
\( w = f(x,y,z). \)
y está sujeta a dos restricciones:
\( g(x,y,z) = 0 \) y \( h(x,y,z) = 0. \)
Existen dos multiplicadores de Lagrange, \( \lambda_1 \) y \( \lambda_2 \), y el sistema de ecuaciones queda de la siguiente forma:
\( \nabla f(x_0,y_0,z_0) = \lambda_1 \nabla g(x_0,y_0,z_0) + \lambda_2 \nabla h(x_0,y_0,z_0) \)
\( g(x_0,y_0,z_0) = 0 \)
\( h(x_0,y_0,z_0) = 0. \)
Ejemplo ilustrativo 11.8.4. Problemas con dos restricciones
Halle los valores extremos locales de la función \( f(x,y,z) = x^2 + y^2 + z^2 \), sujeta a las restricciones \( z^2 = x^2 + y^2 \) y \( x + y – z + 1 = 0 \).
Solución:
Sigamos la estrategia de resolución de problemas:
- La función de optimización es \( f(x, y, z) = x^2 + y^2 + z^2 \). Para determinar las funciones de restricción, primero restamos \( z^2 \) de ambos lados de la primera restricción, lo que nos da \( x^2 + y^2 – z^2 = 0 \), por lo que \( g(x, y, z) = x^2 + y^2 – z^2 \). La segunda función de restricción es \( h(x, y, z) = x + y – z + 1 \).
-
Luego calculamos los gradientes de \( f, g \) y \( h \):
$$\nabla f(x, y, z) = 2x\mathbf{i} + 2y\mathbf{j} + 2z\mathbf{k}$$ $$\nabla g(x, y, z) = 2x\mathbf{i} + 2y\mathbf{j} – 2z\mathbf{k}$$ $$\nabla h(x, y, z) = \mathbf{i} + \mathbf{j} – \mathbf{k}$$
La ecuación \( \nabla f(x_0, y_0, z_0) = \lambda_1 \nabla g(x_0, y_0, z_0) + \lambda_2 \nabla h(x_0, y_0, z_0) \) se convierte en:$$2x_0\mathbf{i} + 2y_0\mathbf{j} + 2z_0\mathbf{k} = \lambda_1 (2x_0\mathbf{i} + 2y_0\mathbf{j} – 2z_0\mathbf{k}) + \lambda_2 (\mathbf{i} + \mathbf{j} – \mathbf{k}),$$
que puede reescribirse como:$$2x_0\mathbf{i} + 2y_0\mathbf{j} + 2z_0\mathbf{k} = (2\lambda_1 x_0 + \lambda_2)\mathbf{i} + (2\lambda_1 y_0 + \lambda_2)\mathbf{j} – (2\lambda_1 z_0 + \lambda_2)\mathbf{k}.$$
A continuación, igualamos los coeficientes de \( \mathbf{i}, \mathbf{j} \) y \( \mathbf{k} \) iguales entre sí:$$2x_0 = 2\lambda_1 x_0 + \lambda_2$$ $$2y_0 = 2\lambda_1 y_0 + \lambda_2$$ $$2z_0 = -2\lambda_1 z_0 – \lambda_2$$
Las dos ecuaciones que surgen de las restricciones son \( z_0^2 = x_0^2 + y_0^2 \) y \( x_0 + y_0 – z_0 + 1 = 0 \). Combinando estas ecuaciones con las tres anteriores obtenemos:$$2x_0 = 2\lambda_1 x_0 + \lambda_2$$ $$2y_0 = 2\lambda_1 y_0 + \lambda_2$$ $$2z_0 = -2\lambda_1 z_0 – \lambda_2$$ $$z_0^2 = x_0^2 + y_0^2$$ $$x_0 + y_0 – z_0 + 1 = 0.$$
-
Las primeras tres ecuaciones contienen la variable \( \lambda_2 \). Resolviendo la tercera ecuación para \( \lambda_2 \) y sustituyéndola en la primera y segunda ecuaciones, reducimos el número de ecuaciones a cuatro:
$$2x_0 = 2\lambda_1 x_0 – 2\lambda_1 z_0 – 2z_0$$ $$2y_0 = 2\lambda_1 y_0 – 2\lambda_1 z_0 – 2z_0$$ $$z_0^2 = x_0^2 + y_0^2$$ $$x_0 + y_0 – z_0 + 1 = 0.$$
A continuación, resolvemos la primera y segunda ecuación para \( \lambda_1 \). La primera ecuación da \( \lambda_1 = \frac{x_0 + z_0}{x_0 – z_0} \), la segunda ecuación da \( \lambda_1 = \frac{y_0 + z_0}{y_0 – z_0} \). Igualamos los lados derechos de cada ecuación y multiplicamos en cruz:
$$\frac{x_0 + z_0}{x_0 – z_0} = \frac{y_0 + z_0}{y_0 – z_0}$$ $$(x_0 + z_0)(y_0 – z_0) = (x_0 – z_0)(y_0 + z_0)$$ $$x_0 y_0 – x_0 z_0 + y_0 z_0 – z_0^2 = x_0 y_0 + x_0 z_0 – y_0 z_0 – z_0^2$$ $$2y_0 z_0 – 2x_0 z_0 = 0$$ $$2z_0(y_0 – x_0) = 0.$$
Por lo tanto, \( z_0 = 0 \) o \( y_0 = x_0 \). Si \( z_0 = 0 \), entonces la primera restricción se convierte en \( 0 = x_0^2 + y_0^2 \). La única solución real para esta ecuación es \( x_0 = 0 \) y \( y_0 = 0 \), lo cual da la terna ordenada \( (0, 0, 0) \). Este punto no satisface la segunda restricción, por lo que no es una solución. A continuación, consideramos \( y_0 = x_0 \), lo que reduce el número de ecuaciones a tres:$$y_0 = x_0$$ $$z_0^2 = x_0^2 + y_0^2$$ $$x_0 + y_0 – z_0 + 1 = 0.$$
Sustituimos la primera ecuación en la segunda y tercera ecuaciones:$$z_0^2 = x_0^2 + x_0^2$$ $$x_0 + x_0 – z_0 + 1 = 0.$$
Luego, resolvemos la segunda ecuación para \( z_0 \), lo que da \( z_0 = 2x_0 + 1 \). Sustituimos esto en la primera ecuación:$$z_0^2 = 2x_0^2$$ $$(2x_0 + 1)^2 = 2x_0^2$$ $$4x_0^2 + 4x_0 + 1 = 2x_0^2$$ $$2x_0^2 + 4x_0 + 1 = 0.$$
Recordando que \( y_0 = x_0 \), esto también resuelve para \( y_0 \). Luego, \( z_0 = 2x_0 + 1 \), de modo que$$z_0 = 2x_0 + 1 = 2\left( -1 \pm \frac{\sqrt{2}}{2} \right) + 1 = -2 + 1 \pm \sqrt{2} = -1 \pm \sqrt{2}.$$
Por lo tanto, hay dos ternas ordenadas como solución:$$\left( -1 + \frac{\sqrt{2}}{2}, -1 + \frac{\sqrt{2}}{2}, -1 + \sqrt{2} \right) \text{ y } \left( -1 – \frac{\sqrt{2}}{2}, -1 – \frac{\sqrt{2}}{2}, -1 – \sqrt{2} \right).$$
-
Sustituimos \( \left( -1 + \frac{\sqrt{2}}{2}, -1 + \frac{\sqrt{2}}{2}, -1 + \sqrt{2} \right) \) en \( f(x, y, z) = x^2 + y^2 + z^2 \), lo que da
$$\begin{aligned} f\left( -1 + \frac{\sqrt{2}}{2}, -1 + \frac{\sqrt{2}}{2}, -1 + \sqrt{2} \right) &= \left( -1 + \frac{\sqrt{2}}{2} \right)^2 + \left( -1 + \frac{\sqrt{2}}{2} \right)^2 + (-1 + \sqrt{2})^2 \\ &= \left( 1 – \sqrt{2} + \frac{1}{2} \right) + \left( 1 – \sqrt{2} + \frac{1}{2} \right) + (1 – 2\sqrt{2} + 2) \\ &= 6 – 4\sqrt{2}. \end{aligned}$$
Luego, sustituimos \( \left( -1 – \frac{\sqrt{2}}{2}, -1 – \frac{\sqrt{2}}{2}, -1 – \sqrt{2} \right) \) en \( f(x, y, z) = x^2 + y^2 + z^2 \), lo que da$$\begin{aligned} f\left( -1 – \frac{\sqrt{2}}{2}, -1 – \frac{\sqrt{2}}{2}, -1 – \sqrt{2} \right) &= \left( -1 – \frac{\sqrt{2}}{2} \right)^2 + \left( -1 – \frac{\sqrt{2}}{2} \right)^2 + (-1 – \sqrt{2})^2 \\ &= \left( 1 + \sqrt{2} + \frac{1}{2} \right) + \left( 1 + \sqrt{2} + \frac{1}{2} \right) + (1 + 2\sqrt{2} + 2) \\ &= 6 + 4\sqrt{2}. \end{aligned}$$
\( 6 + 4\sqrt{2} \) y \( 6 – 4\sqrt{2} \) son los valores extremos locales de \( f(x, y, z) \), sujetos a las restricciones dadas. ♦
Ejercicio de control 11.8.4
Utilice el método de los multiplicadores de Lagrange para hallar el valor mínimo de la función:
$$f(x, y, z) = x^2 + y^2 + z^2$$
sujeta a las restricciones \( 2x + y + 2z = 9 \) y \( 5x + 5y + 7z = 29 \). ♦
