| 9. Ecuaciones diferenciales | 9.7.Soluciones en serie de ecuaciones lineales de segundo orden | Ejercicios propuestos para el Capítulo 9.7.4 |

9.7.5 El método de Frobenius I

En esta sección comenzamos a estudiar soluciones en serie de una ecuación diferencial lineal homogénea de segundo orden con un punto singular regular en x₀ = 0, por lo que se puede escribir como

x²A(x)y′′ + xB(x)y′ + C(x)y = 0,         (9.7.5.1)

donde A, B, C son polinomios y A(0) ≠ 0.

      Veremos que (9.7.5.1) siempre tiene al menos una solución de la forma

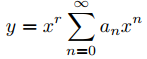
donde a₀ ≠ 0 y r es un número adecuadamente elegido. El método que usaremos para encontrar soluciones de esta forma y otras formas que encontraremos en las próximas dos secciones se llama el método de Frobenius, y las llamaremos soluciones de Frobenius.

      Puede demostrarse que la serie de potencias en una solución de Frobenius de (9.7.5.1) converge en algún intervalo abierto (−ρ, ρ), donde 0 < ρ ≤ ∞. Sin embargo, dado que x^r puede ser complejo para x negativo o indefinido si x = 0, consideraremos soluciones definidas para valores positivos de x. Fáciles modificaciones de nuestros resultados producen soluciones definidas para valores negativos de x. (Ejercicio 54).

      Restringiremos nuestra atención al caso donde A, B y C son polinomios de grado no mayor que dos, por lo que (9.7.5.1) se convierte en

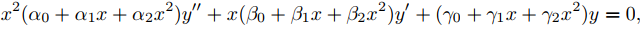      (9.7.5.2)

donde α_i, β_i y γ_i son constantes reales y α₀ ≠ 0. La mayoría de las ecuaciones que surgen en las aplicaciones se pueden escribir de esta manera. Algunos ejemplos son

αx2y′′ + βxy′ + γy = 0 (ecuación de Euler),
x²y′′ + xy′ + (x² − ν²)y = 0 (ecuación de Bessel),

y

xy′′ + (1 − x)y′ + λy = 0, (ecuación de Laguerre),

donde multiplicaríamos la última ecuación por x para ponerla en la forma (9.7.5.2). Sin embargo, el método de Frobenius se puede extender al caso donde A, B y C son funciones que se pueden representar mediante series de potencias en x en algún intervalo que contiene cero, y A₀(0) ≠ 0 (Ejercicios 57 y 58 ).

       Los siguientes dos teoremas nos permitirán desarrollar métodos sistemáticos para encontrar soluciones de Frobenius de (9.7.5.2).

Teorema 9.7.5.1

Sea

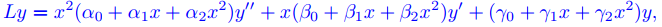
y definimos

Supongamos que la serie

        (9.7.5.3)

converge en (0, ρ). Entonces

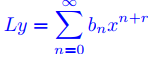        (9.7.5.4)

en (0, ρ), donde

      (9.7.5.5)

Prueba:

Comenzamos demostrando que si y está dada por (9.7.5.3) y α, β y γ son constantes, entonces

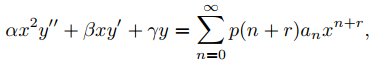       (9.7.5.6)

donde

p(r) = αr(r − 1) + βr + γ.

Derivando (9.7.5.3) dos veces se obtiene

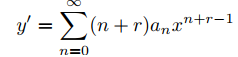        (9.7.5.7)

y

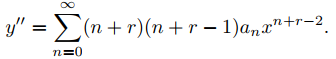        (9.7.5.8)

Multiplicando (9.7.5.7) por x y (9.7.5.8) por x² se obtiene

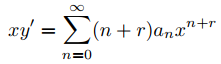
y

Por lo tanto

lo que prueba (9.7.5.6).

      Multiplicando (9.7.5.6) por x se obtiene

      (9.7.5.9)

Multiplicando (9.7.5.6) por x² se obtiene

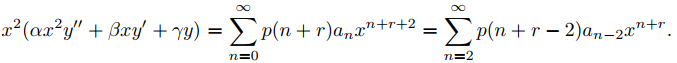      (9.7.5.10)

Para usar estos resultados, reescribimos

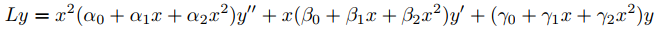
como

      (9.7.5.11)

De (9.7.5.6) con p = p₀,

De (9.7.5.9) con p = p₁,

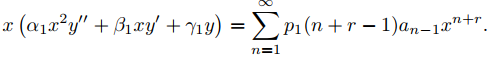
De (9.7.5.10) con p = p₂,

Por lo tanto podemos reescribir (9.7.5.11) como

o

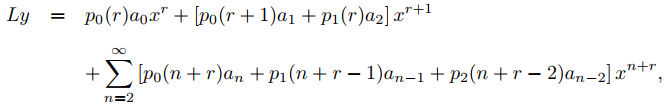
lo que implica (9.7.5.4) con {b_n} definido como en (9.7.5.5).  ♦

Teorema 9.7.5.2

Sea

donde α₀ ≠ 0, y definimos

Supongamos que r es un número real tal que p₀(n + r) es distinto de cero para todos los números enteros positivos n. Definimos

      (9.7.5.12)

Entonces la serie de Frobenius

      (9.7.5.13)

converge y satisface

        (9.7.5.14)

en el intervalo (0, ρ), donde ρ es la distancia del origen al cero más próximo de A(x) = α₀ + α₁x + α₂x² en el plano complejo. (Si A es constante, entonces ρ = ∞.)

      Si {a_n(r)} está determinada por la relación de recurrencia (9.7.5.12), al sustituir a_n = a_n(r) en (9.7.5.5) se obtiene b₀ = p₀(r) y b_n = 0 para n ≥ 1, entonces ( 9.7.5.4) se reduce a (9.7.5.14). Omitimos la prueba de que la serie (9.7.5.13) converge en (0, ρ).  ♦

      Si α_i = β_i = γ_i = 0 para i = 1, 2, entonces L_y = 0 se reduce a la ecuación de Euler

α₀x²y′′ + β₀xy′ + γ₀y = 0.

El Teorema 9.7.4.1 muestra que las soluciones de esta ecuación están determinadas por los ceros del polinomio indicial

p₀(r) = α₀r(r − 1) + β₀r + γ₀.

Como (9.7.5.14) implica que esto también es cierto para las soluciones de L_y = 0, también diremos que p₀ es el polinomio indicial de (9.7.5.2), y que p₀(r) = 0 es la ecuación indicial de L_y = 0. Consideraremos solo los casos donde la ecuación indicial tiene raíces reales r₁ y r₂, con r₁ ≥ r₂.

Teorema 9.7.5.3

Sean L y {a_n(r)} como en el Teorema 9.7.5.2, y suponga que la ecuación indicial p₀(r) = 0 de L_y = 0 tiene raíces reales r₁ y r₂, donde r₁ ≥ r₂. Entonces

es una solución de Frobenius de L_y = 0. Además, si r₁ − r₂ no es un número entero, entonces

es también una solución de Frobenius de L_y = 0, y {y₁, y₂} es un conjunto fundamental de soluciones.  ♦

Prueba:

Dado que r₁ y r₂ son raíces de p₀(r) = 0, el polinomio indicial se puede factorizar como

p₀(r) = α₀(r − r₁)(r − r₂).         (9.7.5.15)

Por lo tanto

p₀(n + r₁) = nα₀(n + r₁ − r₂),

que es distinto de cero si n > 0, ya que r₁ − r₂ ≥ 0. Por lo tanto, los supuestos del Teorema 9.7.5.2 se cumplen con r = r₁, y (9.7.5.14) implica que Ly₁ = p₀(r₁)x^r₁ = 0.

      Ahora suponga que r₁ − r₂ no es un número entero. De (9.7.5.15),

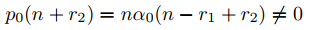  si  n = 1, 2, · · · .

Por tanto, los supuestos del Teorema 9.7.5.2 se cumplen con r = r₂, y (9.7.5.14) implica que Ly₂ = p₀(r₂)x^r₂ = 0 = 0. Dejamos la prueba de que {y₁, y₂} es un conjunto fundamental de soluciones como un ejercicio (Ejercicio 52).  ♦

      No siempre es posible obtener fórmulas explícitas para los coeficientes en las soluciones de Frobenius. Sin embargo, siempre podemos establecer las relaciones de recurrencia y usarlas para calcular tantos coeficientes como queramos.
El siguiente ejemplo ilustra esto.

Ejemplo ilustrativo 9.7.5.1

Encuentre un conjunto fundamental de soluciones de Frobenius de

2x²(1 + x + x²)y′′ + x(9 + 11x + 11x²)y′ + (6 + 10x + 7x²)y = 0.         (9.7.5.16)

Calcule solo los primeros seis coeficientes a₀,. . . , a₅ en cada solución.

Solución:

Para la ecuación dada, los polinomios definidos en el Teorema 9.7.5.2 son

Los ceros del polinomio indicial p₀ son r₁ = −3/2 y r₂ = −2, entonces r₁ − r₂ = 1/2. Por tanto, el Teorema 9.7.5.3 implica que

  y 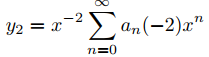         (9.7.5.17)

forman un conjunto fundamental de soluciones de Frobenius de (9.7.5.16). Para encontrar los coeficientes en estas series, usamos la relación de recurrencia del Teorema 9.7.5.2; de este modo,

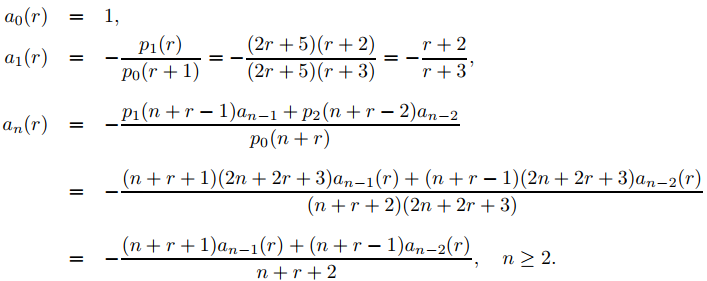
Establecer r = −3/2 en estas ecuaciones produce

        (9.7.5.18)

y estableciendo r = −2 se obtiene

        (9.7.5.19)

Calculando con (9.7.5.18) y (9.7.5.19) y sustituyendo los resultados en (9.7.5.17) se obtiene el conjunto fundamental de soluciones de Frobenius

  ♦

Casos especiales con relaciones de recurrencia de dos términos

Para n ≥ 2, la relación de recurrencia (9.7.5.12) del teorema 9.7.5.2 involucra los tres coeficientes a_n(r), a_{n − 1}(r) y a_{n − 2}(r). Ahora consideraremos algunos casos especiales donde (9.7.5.12) se reduce a una relación de recurrencia de dos términos; es decir, una relación que involucra solo a_n(r) y a_{n − 1}(r) o solo a_n(r) y a_{n − 2}(r). Esta simplificación a menudo hace posible obtener fórmulas explícitas para los coeficientes de las soluciones de Frobenius.

      Primero consideramos ecuaciones de la forma

x²(α₀ + α₁x)y′′ + x(β₀ + β₁x)y′ + (γ₀ + γ₁x)y = 0

con α₀ ≠ 0. Para esta ecuación, α₂ = β₂ = γ₂ = 0, entonces p₂ ≡ 0 y las relaciones de recurrencia en el Teorema 9.7.5.2 se simplifican a

      (9.7.5.20)

Ejemplo ilustrativo 9.7.5.2

Encuentre un conjunto fundamental de soluciones de Frobenius de

x²(3 + x)y′′ + 5x(1 + x)y′ − (1 − 4x)y = 0.         (9.7.5.21)

Dé fórmulas explícitas para los coeficientes en las soluciones.

Solución:

Para esta ecuación, los polinomios definidos en el Teorema 9.7.5.2 son

Los ceros del polinomio indicial p₀ son r₁ = 1/3 y r₂ = −1, entonces r₁ − r₂ = 4/3. Por tanto, el Teorema 9.7.5.3 implica que

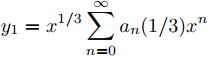  y 

forman un conjunto fundamental de soluciones de Frobenius de (9.7.5.21). Para encontrar los coeficientes en estas series, usamos las relaciones de recurrencias (9.7.5.20); de este modo,

        (9.7.5.22)

Establecer r = 1/3 in (9.7.5.22) produce

Usando la notación de producto presentada en la Sección 9.7.2 y procediendo como lo hicimos en los ejemplos de esa sección, se obtiene

Por lo tanto

es una solución de Frobenius de (9.7.5.21).

      Al establecer r = −1 en (9.7.5.22) se obtiene

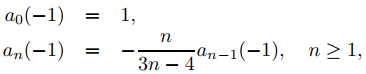
por lo que

Por lo tanto

es una solución de Frobenius de (9.7.5.21), y {y₁, y₂} es un conjunto fundamental de soluciones.  ♦

      Consideremos ahora ecuaciones de la forma

x²(α₀ + α₂x²)x² + x(β₀ + β₂x²)y′ + (γ₀ + γ₂x²)y = 0         (9.7.5.23)

con α₀ ≠ 0. Para esta ecuación, α₁ = β₁ = γ₁ = 0, entonces p₁ ≡ 0 y las relaciones de recurrencia en el Teorema 9.7.5.2 se simplifican a

Dado que a₁(r) = 0, la última ecuación implica que a_n(r) = 0 si n es impar, por lo que las soluciones de Frobenius son de la forma

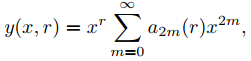
donde

        (9.7.5.24)

Ejemplo ilustrativo 9.7.5.3

Encuentre un conjunto fundamental de soluciones de Frobenius de

x²(2 − x²)y′′ − x(3 + 4x²)y′ + (2 − 2x²)y = 0.         (9.7.5.25)

Dé fórmulas explícitas para los coeficientes en las soluciones.

Solución:

Para esta ecuación, los polinomios definidos en el Teorema 9.7.5.2 son

Los ceros del polinomio indicial p0 son r₁ = 2 y r₂ = 1/2, entonces r₁ − r₂ = 3/2. Por tanto, el Teorema 9.7.5.3 implica que

  y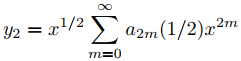 

forman un conjunto fundamental de soluciones de Frobenius de (9.7.5.25). Para encontrar los coeficientes en estas series, usamos la relación de recurrencia (9.7.5.24); de este modo,

        (9.7.5.26)

Establecer r = 2 en (9.7.5.26) produce

así que

Por lo tanto

es una solución de Frobenius de (9.7.5.25).

       Establecer r = 1/2 en (9.7.5.26) produce

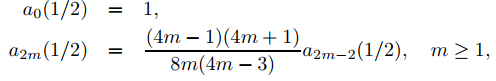
entonces

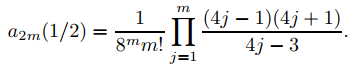
Por lo tanto

es una solución de Frobenius de (9.7.5.25) y {y₁, y₂} es un conjunto fundamental de soluciones.  ♦

OBSERVACIÓN: Hasta ahora, consideramos solo el caso donde la ecuación indicial tiene raíces reales que no difieren en un número entero, lo que nos permite aplicar el Teorema 9.7.5.3. Sin embargo, para ecuaciones de la forma (9.7.5.23), la sucesión {a₂m(r)} en (9.7.5.24) se define para r = r₂ si r₁ − r₂ no es un número entero par. Se puede demostrar (Ejercicio 56) que en este caso

  y 

forman un conjunto fundamental de soluciones de Frobenius de (9.7.5.23).

USO DE TECNOLOGÍA

      Como dijimos al final de la Sección 9.7.2, si está interesado en usar series para calcular aproximaciones numéricas a las soluciones de una ecuación diferencial, entonces si hay o no una forma cerrada simple para los coeficientes es esencialmente irrelevante; el cálculo recursivo suele ser más eficiente. Dado que también es laborioso, lo alentamos a escribir programas cortos para implementar relaciones de recurrencia en una calculadora o computadora, incluso en ejercicios donde esto no se requiere específicamente.

      En el uso práctico del método de Frobenius cuando x₀ = 0 es un punto singular regular, estamos interesados en qué tan bien funcionan las funciones

soluciones aproximadas a una ecuación dada cuando r_i es un cero del polinomio indicial. Al tratar el problema correspondiente para el caso donde x₀ = 0 es un punto ordinario, usamos la integración numérica para resolver la ecuación diferencial sujeta a las condiciones iniciales y(0) = a_0, y′(0) = a₁, y comparamos el resultado con valores del polinomio de Taylor

No podemos hacer eso aquí, ya que en general no podemos prescribir valores iniciales arbitrarios para las soluciones de una ecuación diferencial en un punto singular. Por lo tanto, motivado por el Teorema 9.7.5.2 (específicamente, (9.7.5.14)), sugerimos el siguiente procedimiento.

Procedimiento de verificación

Sean L e Y_n (x; r_i) definidas por

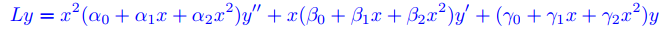
y

donde los coeficientes se calculan como en (9.7.5.12), Teorema 9.7.5.2. Calcular el error

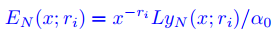        (9.7.5.27)

para varios valores de N y varios valores de x en el intervalo (0, ρ), con ρ como se define en el Teorema 9.7.5.2.  ♦

      El multiplicador x^−r_i/α₀ a la derecha de (9.7.5.27) elimina los efectos de valores pequeños o grandes de x^r_i cerca de x = 0, y de la multiplicación por una constante arbitraria. En algunos ejercicios se le pedirá que estime el valor máximo de E_N(x; r_i) en un intervalo (0, δ] calculando E_N(x_m; r_i) en los M puntos x_m = mδ/M, m = 1, 2 , . . . , M, y encontrando el máximo de los valores absolutos:

σ_N(δ) = máx{|E_N(x_m; r_i)|, m = 1, 2, . . ., M}.         (9.7.5.28)

Por simplicidad, esta notación ignora la dependencia del lado derecho de la ecuación de i y M.)

      Para implementar este procedimiento, tendrá que escribir un programa de computadora para calcular {a_n(r_i)} a partir de la relación de recurrencia aplicable y evaluar E_N(x; r_i).

      El siguiente conjunto de ejercicios contiene cinco ejercicios específicamente identificados por L que le piden que implemente el procedimiento de verificación. Estos ejercicios en particular se eligieron arbitrariamente. También puede formular tales problemas de laboratorio para cualquiera de las ecuaciones en cualquiera de los ejercicios 1 a 10, 14 a 25 y 28 a 51.