12.2 Integrales dobles sobre regiones generales

| 12. Integración múltiple | Ejercicios propuestos para el Capítulo 12.2 |

12.2 Integrales dobles sobre regiones generales

Objetivos de aprendizaje

12.2.1 Reconocer cuándo una función de dos variables es integrable sobre una región general.
12.2.2 Evaluar una integral doble calculando una integral iterada sobre una región limitada por dos rectas verticales y dos funciones de x, o por dos rectas horizontales y dos funciones de y.
12.2.3 Simplificar el cálculo de una integral iterada cambiando el orden de integración.
12.2.4 Usar integrales dobles para calcular el volumen de una región entre dos superficies o el área de una región plana.
12.2.5 Resolver problemas que involucren integrales dobles impropias.

En Integrales dobles sobre regiones rectangulares, estudiamos el concepto de integrales dobles y examinamos las herramientas necesarias para calcularlas. Aprendimos técnicas y propiedades para integrar funciones de dos variables sobre regiones rectangulares. También analizamos varias aplicaciones, como hallar el volumen limitado por una función sobre una región rectangular, encontrar áreas mediante integración y calcular el valor promedio de una función de dos variables.

En esta sección consideramos integrales dobles de funciones definidas sobre una región general acotada D en el plano. La mayoría de los resultados anteriores también se mantienen en esta situación, pero algunas técnicas necesitan ampliarse para cubrir este caso más general.

Regiones generales de integración

Un ejemplo de una región acotada general $ D $ en el plano se muestra en la Figura 12.2.1. Como $ D $ está acotada en el plano, debe existir una región rectangular $ R $ en el mismo plano que encierre a la región $ D $; es decir, existe una región rectangular $ R $ tal que $ D $ es un subconjunto de $ R $ $(D \subseteq R)$.

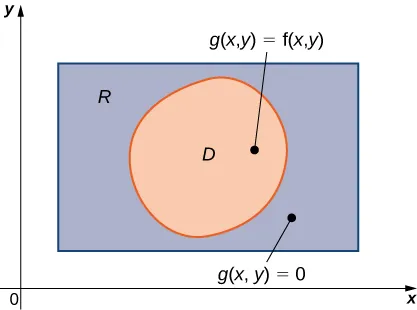
Figura 12.2.1 Para una región $ D $ que es un subconjunto de $ R $, podemos definir una función $ g(x,y) $ que sea igual a $ f(x,y) $ en cada punto de $ D $ y 0 en cada punto de $ R $ que no pertenece a $ D $.

Suponga que $ z = f(x, y) $ está definida en una región plana acotada general $ D $, como en la Figura 12.2.1. Para desarrollar integrales dobles de $ f $ sobre $ D $, extendemos la definición de la función para incluir todos los puntos en la región rectangular $ R $ y luego utilizamos los conceptos y herramientas de la sección precedente. Pero, ¿cómo extendemos la definición de $ f $ para incluir todos los puntos en $ R $? Lo hacemos definiendo una nueva función $ g(x, y) $ en $ R $ de la siguiente manera:

\[ g(x, y) = \begin{cases} f(x, y) & \text{si } (x, y) \text{ está en } D \\ 0 & \text{si } (x, y) \text{ está en } R \text{ pero no en } D \end{cases} \]

Tenga en cuenta que podríamos tener algunas dificultades técnicas si el contorno de $ D $ es complicado. Por lo tanto, asumimos que el contorno es una curva cerrada simple, continua y suave por tramos. Además, dado que todos los resultados desarrollados en Integrales Dobles sobre Regiones Rectangulares utilizaron una función integrable $ f(x, y) $, debemos tener cuidado con $ g(x, y) $ y verificar que $ g(x, y) $ sea una función integrable sobre la región rectangular $ R $. Esto ocurre siempre que la región $ D $ esté acotada por curvas cerradas simples. Por ahora, nos concentraremos en las descripciones de las regiones más que en la función y extenderemos nuestra teoría de manera apropiada para la integración.

Consideramos dos tipos de regiones planas acotadas.

Definición

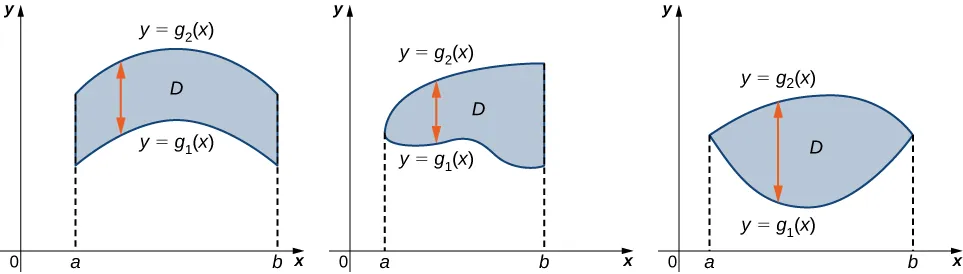
Una región $ D $ en el plano $ (x, y) $ es de Tipo I si se encuentra entre dos líneas verticales y las gráficas de dos funciones continuas $ g_1(x) $ y $ g_2(x) $. Esto es (Figura 12.2.2),

\[ D = \{ (x, y) \mid a \leq x \leq b, g_1(x) \leq y \leq g_2(x) \} \]

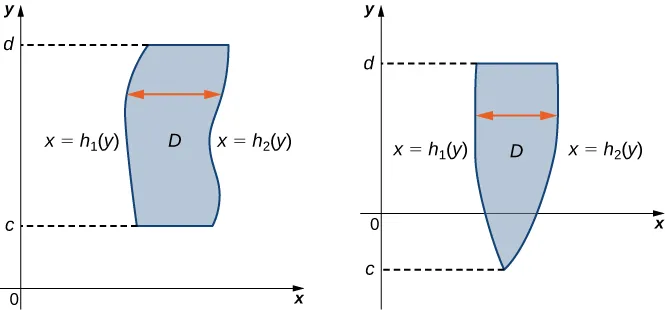
Una región $ D $ en el plano $ xy $ es de Tipo II si se encuentra entre dos líneas horizontales y las gráficas de dos funciones continuas $ h_1(y) $ y $ h_2(y) $. Esto es (Figura 12.2.3),

\[ D = \{ (x, y) \mid c \leq y \leq d, h_1(y) \leq x \leq h_2(y) \} \]

♦

**Figura 12.2.2** Una región de Tipo I se encuentra entre dos rectas verticales y las gráficas de dos funciones de x.

**Figura 12.2.3** Una región de Tipo II se encuentra entre dos rectas horizontales y las gráficas de dos funciones de y.

Ejemplo ilustrativo 12.2.1. Descripción de una Región como Tipo I y También como Tipo II

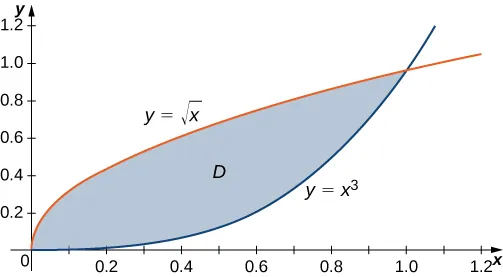
Considere la región en el primer cuadrante entre las funciones $ y=\sqrt{x} $ y $ y=x^3 $ (Figura 12.2.4). Describa la región primero como de Tipo I y luego como de Tipo II.

**Figura 12.2.4** La Región D puede describirse como Tipo I o como Tipo II.

Solución:

Al describir una región como de Tipo I, necesitamos identificar la función que se encuentra arriba de la región y la función que se encuentra debajo de la región. Aquí, la región $ D $ está acotada arriba por $ y = \sqrt{x} $ y abajo por $ y = x^3 $ en el intervalo para $ x $ en $ [0, 1] $. Por lo tanto, como Tipo I, $ D $ se describe como el conjunto:

\[ \{ (x, y) \mid 0 \leq x \leq 1, x^3 \leq y \leq \sqrt{x} \} \]

Sin embargo, al describir una región como de Tipo II, necesitamos identificar la función que se encuentra a la izquierda de la región y la función que se encuentra a la derecha de la región. Aquí, la región $ D $ está acotada a la izquierda por $ x = y^2 $ y a la derecha por $ x = \sqrt[3]{y} $ en el intervalo para $ y $ en $ [0, 1] $. Por lo tanto, como Tipo II, $ D $ se describe como el conjunto:

\[ \{ (x, y) \mid 0 \leq y \leq 1, y^2 \leq x \leq \sqrt[3]{y} \} \]

♦

Ejercicio de control 12.2.1

Considere la región en el primer cuadrante entre las funciones $ y=2x $ y $ y=x^2 $. Describa la región primero como de Tipo I y luego como de Tipo II. ♦

Integrales Dobles sobre Regiones No Rectangulares

Para desarrollar el concepto y las herramientas para evaluar una integral doble sobre una región general no rectangular, primero necesitamos comprender la región y ser capaces de expresarla como Tipo I, Tipo II o una combinación de ambas. Sin comprender las regiones, no podremos determinar los límites de integración en las integrales dobles. Como primer paso, observemos el siguiente teorema.

Teorema 12.2.1. Integrales Dobles sobre Regiones No Rectangulares

Suponga que $ g(x, y) $ es la extensión al rectángulo $ R $ de la función integrable $ f(x, y) $ definida en la región $ D $, donde $ D $ está contenida en $ R $. Las regiones de muestra se muestran en la Figura 12.2.1 . Entonces $ g(x, y) $ es integrable y definimos la integral doble de $ f(x, y) $ sobre $ D $ mediante:

\[ \iint_D f(x, y) \, dA = \iint_R g(x, y) \, dA \]

♦

El lado derecho de esta ecuación es lo que ya hemos visto antes, por lo tanto, este teorema es razonable porque $ R $ es un rectángulo y $ \iint_R g(x,y)\,dA $ se ha discutido en la sección anterior. Además, la igualdad funciona porque los valores de $ g(x,y) $ son 0 para cualquier punto $ (x,y) $ que se encuentre fuera de $ D $, y por lo tanto, estos puntos no aportan nada a la integral. Sin embargo, es importante que el rectángulo $ R $ contenga a la región $ D $. Como cuestión de hecho, si la región $ D $ está limitada por curvas suaves en el plano y podemos describirla como de Tipo I o Tipo II o una combinación de ambas, entonces podemos usar el siguiente teorema y no tener que encontrar un rectángulo $ R $ que contenga a la región.

Teorema 12.2.2. Teorema de Fubini (Forma Fuerte)

Para una función $ f(x, y) $ que es continua en una región $ D $ de Tipo I, tenemos

\[ \iint_D f(x, y) \, dA = \iint_D f(x, y) \, dy \, dx = \int_a^b \left[ \int_{g_1(x)}^{g_2(x)} f(x, y) \, dy \right] dx. \]

12.2.1

De manera similar, para una función $ f(x, y) $ que es continua en una región $ D $ de Tipo II, tenemos

\[ \iint_D f(x, y) \, dA = \iint_D f(x, y) \, dx \, dy = \int_c^d \left[ \int_{h_1(y)}^{h_2(y)} f(x, y) \, dx \right] dy. \]

12.2.2

♦

La integral en cada una de estas expresiones es una integral iterada, similar a las que hemos visto antes. Observe que, en la integral interna de la primera expresión, integramos $ f(x,y) $ manteniendo $ x $ constante y siendo los límites de integración $ g_1(x) $ y $ g_2(x) $. En la integral interna de la segunda expresión, integramos $ f(x,y) $ manteniendo $ y $ constante y siendo los límites de integración $ h_1(x) $ y $ h_2(x) $.

Ejemplo ilustrativo 12.2.2. Evaluación de una Integral Iterada sobre una Región Tipo I

Evalúe la integral $\iint_{D} x^2 e^{xy}\, dA$, donde $D$ se muestra en la Figura 12.2.5.

Solución:

Primero construya la región $ D $ como una región de Tipo I (Figura 12.2.5). Aquí $ D = \{ (x, y) \mid 0 \leq x \leq 2, \frac{1}{2}x \leq y \leq 1 \} $. Entonces tenemos

\[ \iint_D x^2 e^{xy} \, dA = \int_{x=0}^{x=2} \int_{y=1/2x}^{y=1} x^2 e^{xy} \, dy \, dx. \]

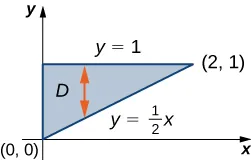
Figura 12.2.5 Podemos expresar la región $D$ como una región de Tipo I e integrar desde $y=\frac{1}{2}x$ hasta $y=1$, entre las rectas $x=0$ y $x=2$.

Por lo tanto, tenemos el siguiente desarrollo para evaluar la integral doble sobre la región de Tipo I:

$$\begin{aligned} &\int_{x=0}^{x=2} \int_{y=1/2x}^{y=1} x^2 e^{xy} \, dy \, dx \\ &= \int_{x=0}^{x=2} \left[ \int_{y=1/2x}^{y=1} x^2 e^{xy} \, dy \right] dx && \text{Integral iterada para una región de Tipo I.} \\ &= \int_{x=0}^{x=2} \left[ x^2 \frac{e^{xy}}{x} \right] \bigg|_{y=1/2x}^{y=1} dx && \text{Integrar respecto a } y \text{ usando sustitución } u=xy \text{ (con } x \text{ constante).} \\ &= \int_{x=0}^{x=2} [x e^x – x e^{x^2/2}] \, dx && \text{Evaluar los límites de integración para } y. \\ &= \left[ x e^x – e^x – e^{\frac{1}{2}x^2} \right] \bigg|_{x=0}^{x=2} && \text{Integrar respecto a } x \text{ (usando sustitución } u=\frac{1}{2}x^2 \text{ en el segundo término).} \\ &= [2e^2 – e^2 – e^2] – [0 – e^0 – e^0] \\ &= [0] – [-1 – 1] \\ &= 2. \end{aligned}$$

♦

En el Ejemplo 12.2.2, podríamos haber considerado la región de otra manera, como $D=\{(x,y)\mid 0\le y\le 1,\; 0\le x\le 2y\}$ (Figura 12.2.6).

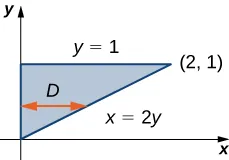
Esta es una región de Tipo II y la integral se vería entonces de la siguiente manera:

$$\begin{aligned} \iint_D x^2 e^{xy} \, dA &= \int_{y=0}^{y=1} \int_{x=0}^{x=2y} x^2 e^{xy} \, dx \, dy. \end{aligned}$$

Sin embargo, si integramos primero con respecto a $ x $, esta integral es larga de calcular porque tenemos que usar integración por partes dos veces.

Ejemplo ilustrativo 12.2.3. Evaluación de una Integral Iterada sobre una Región Tipo II

Evalúe la integral $\iint_D (3x^2+y^2)\,dA$, donde $D=\{(x,y)\mid -2\le y\le 3,\; y^2-3\le x\le y+3\}$.

Solución:

Observe que $D$ puede verse como una región de Tipo I o de Tipo II, como se muestra en la Figura 5.18. Sin embargo, en este caso describir $D$ como región de Tipo I es más complicado que describirla como región de Tipo II. Por lo tanto, usamos $D$ como una región de Tipo II para la integración.

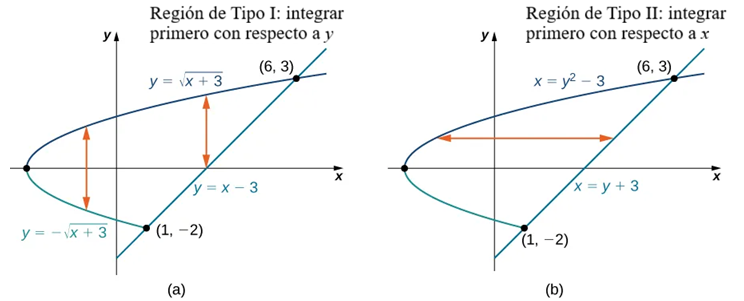
**Figura 12.2.7** La región (D) en este ejemplo puede ser (a) de Tipo I o (b) de Tipo II.

Al elegir este orden de integración, tenemos el siguiente desarrollo para evaluar la integral doble sobre una región de Tipo II:

$$\begin{aligned} &\iint_D (3x^2 + y^2) \, dA \\ &= \int_{y=-2}^{y=3} \int_{x=y^2-3}^{x=y+3} (3x^2 + y^2) \, dx \, dy && \text{Integral iterada, región de Tipo II.} \\ &= \int_{y=-2}^{y=3} (x^3 + xy^2) \bigg|_{y^2-3}^{y+3} \, dy && \text{Integrar con respecto a } x. \\ &= \int_{y=-2}^{y=3} \left( (y+3)^3 + (y+3)y^2 – (y^2-3)^3 – (y^2-3)y^2 \right) dy \\ &= \int_{-2}^{3} (54 + 27y – 12y^2 + 2y^3 + 8y^4 – y^6) \, dy && \text{Integrar con respecto a } y. \\ &= \left[ 54y + \frac{27y^2}{2} – 4y^3 + \frac{y^4}{2} + \frac{8y^5}{5} – \frac{y^7}{7} \right] \bigg|_{-2}^{3} \\ &= \frac{2375}{7}. \end{aligned}$$

♦

Ejercicio de control 12.2.2

Bosqueje la región $D$ y evalúe la integral iterada $\iint_D x y \, dy \, dx$, donde $D$ es la región limitada por las curvas $y=\cos x$ y $y=\sin x$ en el intervalo $\left[-\frac{3\pi}{4},\frac{\pi}{4}\right]$. ♦