| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.19 |

10.19 El teorema de la divergencia

Objetivos de aprendizaje:

10.19.1 Explicar el significado del teorema de la divergencia.
10.19.2 Usar el teorema de la divergencia para calcular el flujo de un campo vectorial.
10.19.3 Aplicar el teorema de la divergencia a un campo electrostático.

Resumen de los Teoremas

Antes de examinar el teorema de la divergencia, es útil comenzar con una descripción general de las versiones del Teorema Fundamental del Cálculo que hemos discutido:

1. El Teorema Fundamental del Cálculo: \[ \int_a^b f'(x) \, dx = f(b) – f(a). \]

   Este teorema relaciona la integral de la derivada \(f’\) sobre el segmento de línea \([a, b]\) a lo largo del eje x con una diferencia de \(f\) evaluada en la frontera.

2. El Teorema Fundamental para Integrales de Línea: \[ \int_C \nabla f \cdot d\mathbf{r} = f(P_1) – f(P_0), \]

   donde \(P_0\) es el punto inicial de \(C\) y \(P_1\) es el punto terminal de \(C\). El Teorema Fundamental para Integrales de Línea permite que el camino \(C\) sea un camino en un plano o en el espacio, no solo un segmento de línea sobre el eje x. Si pensamos en el gradiente como una derivada, entonces este teorema relaciona una integral de la derivada \(\nabla f\) sobre el camino \(C\) con una diferencia de \(f\) evaluada en la frontera de \(C\).

3. El teorema de Green, forma de circulación: \[ \iint_D (Q_x – P_y) \, dA = \oint_C \mathbf{F} \cdot d\mathbf{r}. \]

   Dado que \(Q_x – P_y = \text{rot} \, \mathbf{F} \cdot \mathbf{k}\) y rotacional es una derivada de algún tipo, el teorema de Green relaciona la integral de la derivada rotacional \(\text{rot} \, \mathbf{F}\) sobre la región plana \(D\) a una integral de \(\mathbf{F}\) sobre la frontera de \(D\).

4. El teorema de Green, forma de flujo: \[ \iint_D (P_x + Q_y) \, dA = \oint_C \mathbf{F} \cdot \mathbf{N} \, ds. \]

   Dado que \(P_x + Q_y = \text{div} \, \mathbf{F}\) y divergencia es una derivada de algún tipo, la forma de flujo del teorema de Green relaciona la integral de la derivada de divergencia \(\text{div} \, \mathbf{F}\) sobre la región plana \(D\) a una integral de \(\mathbf{F}\) sobre la frontera de \(D\).

5. El teorema de Stokes: \[ \iint_S \text{rot} \, \mathbf{F} \cdot d\mathbf{S} = \oint_C \mathbf{F} \cdot d\mathbf{r}. \]

   Si pensamos en el rotacional como una derivada de algún tipo, entonces el teorema de Stokes relaciona la integral de la derivada rotacional \(\text{rot} \, \mathbf{F}\) sobre la superficie \(S\) (no necesariamente plana) a una integral de \(\mathbf{F}\) sobre la frontera de \(S\).

Enunciando el Teorema de la Divergencia

El teorema de la divergencia sigue el patrón general de estos otros teoremas. Si pensamos en la divergencia como una especie de derivada, entonces el teorema de la divergencia relaciona una integral triple de la derivada divF sobre un sólido con una integral de flujo de F sobre la frontera del sólido. Más específicamente, el teorema de la divergencia relaciona una integral de flujo del campo vectorial F sobre una superficie cerrada S con una integral triple de la divergencia de F sobre el sólido encerrado por S.

Teorema 10.19.1: El Teorema de la Divergencia

Sea \(S\) una superficie cerrada suave a trozos que encierra el sólido \(E\) en el espacio. Suponga que \(S\) está orientada hacia afuera, y sea \(\mathbf{F}\) un campo vectorial con derivadas parciales continuas en una región abierta que contiene \(E\) (Figura 6.87). Entonces

\[ \iiint_E \text{div} \, \mathbf{F} \, dV = \iint_S \mathbf{F} \cdot d\mathbf{S}. \hspace{20pt} \text{(Ecuación 10.19.1)} \]

♦

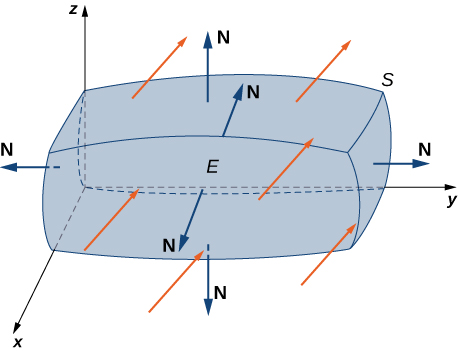
Figura 10.19.1 El teorema de la divergencia relaciona una integral de flujo a través de una superficie cerrada S con una integral triple sobre el sólido E encerrado por la superficie.

Recordemos que la forma de flujo del teorema de Green establece que \(\oint_D \text{div} \, \mathbf{F} \, dA = \oint_C \mathbf{F} \cdot \mathbf{N} \, ds\). Por lo tanto, el teorema de la divergencia es una versión del teorema de Green en una dimensión superior.

La prueba del teorema de la divergencia está fuera del alcance de este texto. Sin embargo, observamos una prueba informal que da una idea general de por qué el teorema es cierto, pero no prueba el teorema con total rigor. Esta explicación sigue la explicación informal dada de por qué el teorema de Stokes es cierto.

Prueba:

Sea \(B\) una pequeña caja con lados paralelos a los planos de coordenadas dentro de \(E\) (Figura 10.19.2). Sea el centro de \(B\) tenga coordenadas \((x, y, z)\) y suponga que las longitudes de los bordes son \(\Delta x\), \(\Delta y\), y \(\Delta z\) (Figura 10.19.2(b)). El vector normal que sale de la parte superior de la caja es \(\mathbf{k}\) y el vector normal que sale de la parte inferior de la caja es \(-\mathbf{k}\). El producto punto de \(\mathbf{F} = \langle P, Q, R \rangle\) con \(\mathbf{k}\) es \(R\) y el producto punto con \(-\mathbf{k}\) es \(-R\). El área de la parte superior de la caja (y la parte inferior de la caja) \(\Delta S\) es \(\Delta x \Delta y\).

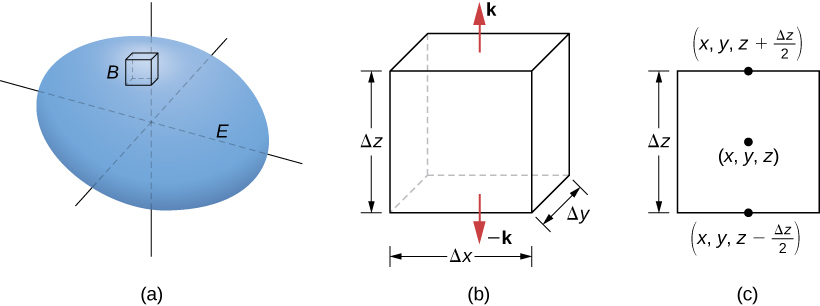
Figura 10.19.2 (a) Una pequeña caja \( B \) dentro de la superficie \( E \) tiene lados paralelos a los planos coordenados. (b) La caja \( B \) tiene longitudes de lado \( \Delta x, \Delta y, \) y \( \Delta z \). (c) Si observamos la vista lateral de \( B \), vemos que, dado que \( (x, y, z) \) es el centro de la caja, para llegar a la parte superior de la caja debemos recorrer una distancia vertical de \( \Delta z/2 \) hacia arriba desde \( (x, y, z) \). De manera similar, para llegar a la parte inferior de la caja debemos recorrer una distancia \( \Delta z/2 \) hacia abajo desde \( (x, y, z) \).

El flujo que sale de la parte superior de la caja se puede aproximar por \(R\left(x, y, z + \frac{\Delta z}{2}\right) \Delta x \Delta y\) (Figura 10.19.2(c)) y el flujo que sale de la parte inferior de la caja es \(-R\left(x, y, z – \frac{\Delta z}{2}\right) \Delta x \Delta y\). Si denotamos la diferencia entre estos valores como \(\Delta R\), entonces el flujo neto en la dirección vertical se puede aproximar por \(\Delta R \Delta x \Delta y\). Sin embargo,

\[ \Delta R \Delta x \Delta y = \left(\frac{\Delta R}{\Delta z}\right) \Delta x \Delta y \Delta z \approx \left(\frac{\partial R}{\partial z}\right) \Delta V. \]

Por lo tanto, el flujo neto en la dirección vertical se puede aproximar por \(\left(\frac{\partial R}{\partial z}\right) \Delta V\). Similarmente, el flujo neto en la dirección x se puede aproximar por \(\left(\frac{\partial P}{\partial x}\right) \Delta V\) y el flujo neto en la dirección y se puede aproximar por \(\left(\frac{\partial Q}{\partial y}\right) \Delta V\). Sumando los flujos en las tres direcciones da una aproximación del flujo total que sale de la caja:

\[ \text{Flujo Total} \approx \left(\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}\right) \Delta V = \text{div} \, \mathbf{F} \Delta V. \]

Esta aproximación se acerca arbitrariamente al valor del flujo total a medida que el volumen de la caja se reduce a cero.

La suma de \(\text{div} \, \mathbf{F} \Delta V\) sobre todas las cajas pequeñas que aproximan \(E\) es aproximadamente \(\iiint_E \text{div} \, \mathbf{F} \, dV\). Por otro lado, la suma de \(\text{div} \, \mathbf{F} \Delta V\) sobre todas las cajas pequeñas que aproximan \(E\) es la suma de los flujos sobre todas estas cajas. Al igual que en la prueba informal del teorema de Stokes, agregar estos flujos sobre todas las cajas resulta en la cancelación de muchos de los términos. Si una caja de aproximación comparte una cara con otra caja de aproximación adyacente, entonces el flujo sobre una cara es el negativo del flujo sobre la cara compartida de la caja adyacente. Estas dos integrales se cancelan. Al sumar todos los flujos, las únicas integrales de flujo que sobreviven son las integrales sobre las caras que aproximan la frontera de \(E\). A medida que los volúmenes de las cajas de aproximación se reducen a cero, esta aproximación se acerca arbitrariamente al flujo sobre \(S\). ♦

Ejemplo ilustrativo 10.19.1: Verificando el Teorema de la Divergencia

Verifica el teorema de la divergencia para el campo vectorial \(\mathbf{F} = \langle x – y, x + z, z – y \rangle\) y la superficie \(S\) que consiste en el cono \(x^2 + y^2 = z^2\), \(0 \leq z \leq 1\), y la parte circular superior del cono (ver la siguiente figura). Asume que esta superficie está orientada hacia afuera.

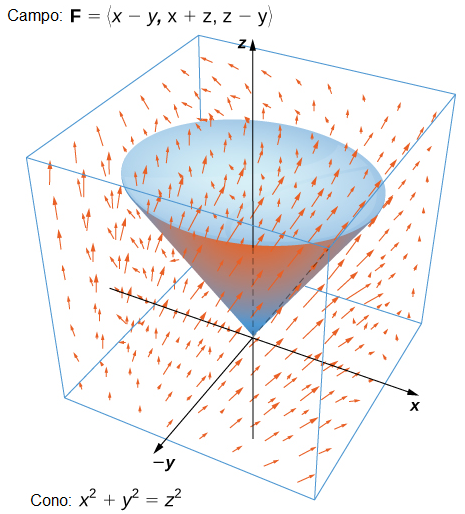
Solución:

Verificar el teorema de la divergencia para el campo vectorial \(\mathbf{F} = \langle x – y, x + z, z – y \rangle\) y la superficie \(S\) que consiste en el cono \(x^2 + y^2 = z^2\), \(0 \leq z \leq 1\), y la parte superior circular del cono (vea la siguiente figura). Asuma que esta superficie está orientada hacia afuera.

Sea \(E\) el cono sólido encerrado por \(S\). Para verificar el teorema para este ejemplo, mostramos que

\[ \iiint_E \text{div} \, \mathbf{F} \, dV = \iint_S \mathbf{F} \cdot d\mathbf{S} \]

calculando cada integral por separado. Nótese que la integral de la derecha es una integral de superficie *cerrada* sobre la superficie S.

Para calcular la integral triple, note que \(\text{div} \, \mathbf{F} = P_x + Q_y + R_z = 2\), y por lo tanto la integral triple es

\[ \iiint_E \text{div} \, \mathbf{F} \, dV = \iiint_E 2 \, dV = 2 (\text{volumen de } E). \]

El volumen de un cono circular recto es \(\pi r^2 \frac{h}{3}\). En este caso, \(h = r = 1\). Por lo tanto,

\[ \iiint_E \text{div} \, \mathbf{F} \, dV = 2(\text{volumen de } E) = \frac{2\pi}{3}. \]

Para calcular la integral de flujo, primero note que \(S\) es suave a trozos; \(S\) se puede escribir como la unión de superficies suaves. Por lo tanto, dividimos la integral de flujo en dos piezas: una integral de flujo a través de la parte superior circular del cono y una integral de flujo a través del resto restante del cono. Llame a la parte superior circular \(S_1\) y a la porción bajo ella \(S_2\). Comenzamos calculando el flujo a través de la parte superior circular del cono. Note que \(S_1\) tiene la parametrización

\[ \mathbf{r}(u, v) = \langle u \cos v, u \sin v, 1 \rangle, 0 \leq u \leq 1, 0 \leq v < 2\pi. \]

Entonces, los vectores tangentes son \(\mathbf{t}_u = \langle \cos v, \sin v, 0 \rangle\) y \(\mathbf{t}_v = \langle -u \sin v, u \cos v, 0 \rangle\). Por lo tanto, el flujo a través de \(S_1\) es

\[ \begin{aligned} \iint_{S_1} \mathbf{F} \cdot d\mathbf{S} &= \int_{0}^{1} \int_{0}^{2\pi} \mathbf{F}(\mathbf{r}(u, v)) \cdot (\mathbf{t}_u \times \mathbf{t}_v) \, dA \\ &= \int_{0}^{1} \int_{0}^{2\pi} \langle u \cos v – u \sin v, u \cos v + 1, 1 – u \sin v \rangle \cdot \langle 0, 0, u \rangle \, dv \, du \\ &= \int_{0}^{1} \int_{0}^{2\pi} u – u \sin v \, dv \, du \\ &= \int_{0}^{1} u – u^2 \sin v \, dv \, du = \pi. \end{aligned} \]

Ahora calculamos el flujo sobre \(S_2\). Una parametrización de esta superficie es

\[ \mathbf{r}(u, v) = \langle u \cos v, u \sin v, u \rangle, 0 \leq u \leq 1, 0 \leq v < 2\pi. \]

Los vectores tangentes son \(\mathbf{t}_u = \langle \cos v, \sin v, 1 \rangle\) y \(\mathbf{t}_v = \langle -u \sin v, u \cos v, 0 \rangle\), así que el producto cruz es

\[ \mathbf{t}_u \times \mathbf{t}_v = \langle -u \cos v, -u \sin v, u \rangle. \]

Note que los signos negativos en las componentes x e y inducen la orientación hacia adentro del cono. Dado que la superficie está orientada hacia afuera, usamos el vector \(\mathbf{t}_u \times \mathbf{t}_v = \langle u \cos v, u \sin v, -u \rangle\) en la integral de flujo. Entonces, el flujo a través de \(S_2\) es

\[ \begin{aligned} \iint_{S_2} \mathbf{F} \cdot d\mathbf{S} &= \int_{0}^{1} \int_{0}^{2\pi} \mathbf{F}(\mathbf{r}(u, v)) \cdot (\mathbf{t}_u \times \mathbf{t}_v) \, dA \\ &= \int_{0}^{1} \int_{0}^{2\pi} \langle u \cos v – u \sin v, u \cos v + u, u – u \sin v \rangle \cdot \langle u \cos v, u \sin v, -u \rangle \, dv \, du \\ &= \int_{0}^{1} \int_{0}^{2\pi} u^2 \cos^2 v – u^2 \sin v \cos v + u^2 \cos v \sin v + u^2 \sin v – u^2 \, dv \, du = -\frac{\pi}{3}. \end{aligned} \]

El flujo total a través de \(S\) es

\[ \iint_S \mathbf{F} \cdot d\mathbf{S} = \iint_{S_1} \mathbf{F} \cdot d\mathbf{S} + \iint_{S_2} \mathbf{F} \cdot d\mathbf{S} = \frac{2\pi}{3} = \iiint_E \text{div} \, \mathbf{F} \, dV, \]

y hemos verificado el teorema de la divergencia para este ejemplo. ♦

Ejercicio de control 10.19.1

Verifica el teorema de la divergencia para el campo vectorial \(\mathbf{F}(x, y, z) = \langle x + y + z, y, 2x – y \rangle\) y la superficie \(S\) dada por el cilindro \(x^2 + y^2 = 1\), \(0 \leq z \leq 3\), más la parte circular superior e inferior del cilindro. Asume que \(S\) está orientada hacia afuera. ♦

Recuerda que la divergencia de un campo continuo \( \mathbf{F} \) en un punto \( P \) es una medida de la “salida” del campo en \( P \). Si \( \mathbf{F} \) representa el campo de velocidad de un fluido, entonces la divergencia puede interpretarse como la tasa por unidad de volumen del fluido que fluye hacia afuera menos la tasa por unidad de volumen que fluye hacia adentro. El teorema de la divergencia confirma esta interpretación. Para ver esto, sea \( P \) un punto y sea \( B_r \) una bola de radio pequeño \( r \) centrada en \( P \) (Figura 10.19.3). Sea \( S_r \) la esfera límite de \( B_r \). Dado que el radio es pequeño y \( \mathbf{F} \) es continuo, \(\text{div } \mathbf{F}(Q) \approx \text{div } \mathbf{F}(P) \) para todos los demás puntos \( Q \) en la bola. Por lo tanto, el flujo a través de \( S_r \) puede aproximarse usando el teorema de la divergencia:

\[ \iint_{S_r} \mathbf{F} \cdot d\mathbf{S} = \iiint_{B_r} \text{div } \mathbf{F} \, dV \approx \iiint_{B_r} \text{div } \mathbf{F}(P) \, dV. \]

Dado que \(\text{div } \mathbf{F}(P) \) es una constante,

\[ \iiint_{B_r} \text{div } \mathbf{F}(P) \, dV = \text{div } \mathbf{F}(P) V(B_r). \]

Por lo tanto, el flujo \(\iint_{S_r} \mathbf{F} \cdot d\mathbf{S} \) puede aproximarse por \(\text{div } \mathbf{F}(P) V(B_r) \). Esta aproximación mejora a medida que el radio se reduce a cero, y por lo tanto

\[ \text{div } \mathbf{F}(P) = \lim_{r \to 0} \frac{1}{V(B_r)} \iint_{S_r} \mathbf{F} \cdot d\mathbf{S}. \]

Esta ecuación dice que la divergencia en \( P \) es la tasa neta de flujo saliente del fluido por unidad de volumen.

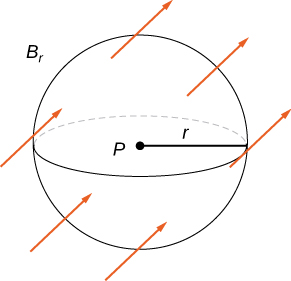
Figura 10.19.3 Bola B_r de radio pequeño r centrada en P.

Usando el Teorema de la Divergencia

El teorema de la divergencia traduce entre la integral de flujo de la superficie cerrada S y una integral triple sobre el sólido encerrado por S. Por lo tanto, el teorema nos permite calcular integrales de flujo o integrales triples que normalmente serían difíciles de calcular traduciendo la integral de flujo en una integral triple y viceversa.

Ejemplo ilustrativo 10.19.2: Aplicando el Teorema de la Divergencia

Calcula la integral de superficie \(\displaystyle \iint_S \mathbf{F} \cdot d\mathbf{S}\), donde \( S \) es el cilindro \( x^2 + y^2 = 1, 0 \leq z \leq 2 \), incluyendo la parte circular superior e inferior, y

\[ \mathbf{F} = \left\langle \frac{x^3}{3} + yz, \frac{y^3}{3} – \sin{(xz)}, z – x – y \right\rangle. \]

Solución:

Podríamos calcular esta integral sin el teorema de la divergencia, pero el cálculo no es sencillo porque tendríamos que dividir la integral de flujo en tres integrales separadas: una para la parte superior del cilindro, una para la parte inferior y otra para el lado. Además, cada integral requeriría parametrizar la superficie correspondiente, calcular los vectores tangentes y su producto cruz, y usar la Ecuación 10.17.1.

Por el contrario, el teorema de la divergencia nos permite calcular la única integral triple \(\displaystyle \iiint_E \text{div} \, \mathbf{F} \, dV\), donde \(E\) es el sólido encerrado por el cilindro. Usando el teorema de la divergencia y convirtiendo a coordenadas cilíndricas, tenemos

\[ \begin{aligned} \iint_S \mathbf{F} \cdot d\mathbf{S} &= \iiint_E \text{div} \, \mathbf{F} \, dV \\ &= \iiint_E (x^2 + y^2 + 1) \, dV \\ &= \int_{0}^{2\pi} \int_{0}^{1} \int_{0}^{2} (r^2 + 1) r \, dz \, dr \, d\theta \\ &= \frac{3}{2} \int_{0}^{2\pi} d\theta = 3\pi. \end{aligned} \]

♦

Ejercicio de control 10.19.2

Use el teorema de la divergencia para calcular la integral de flujo \(\displaystyle \iint_S \mathbf{F} \cdot d\mathbf{S}\), donde \(S\) es la frontera de la caja dada por \(0 \leq x \leq 2\), \(1 \leq y \leq 4\), \(0 \leq z \leq 1\), y \(\mathbf{F} = \langle x^2 + yz, y – z, 2x + 2y + 2z \rangle\) (vea la siguiente figura).

♦

Ejemplo ilustrativo 10.19.3: Aplicando el Teorema de la Divergencia

Sea \(\mathbf{v} = \left\langle -\frac{y}{z}, \frac{x}{z}, 0 \right\rangle\) el campo de velocidad de un fluido. Sea \(C\) el cubo sólido dado por \(1 \leq x \leq 4\), \(2 \leq y \leq 5\), \(1 \leq z \leq 4\), y sea \(S\) la frontera de este cubo (vea la siguiente figura). Encuentre la tasa de flujo del fluido a través de \(S\).

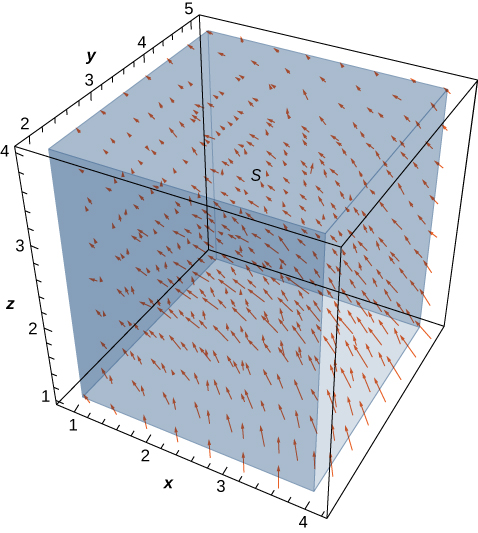
Figura 10.19.4 Campo vectorial \( \mathbf{v} = \left\langle -\frac{y}{z}, \frac{z}{z}, 0 \right\rangle \).

Solución:

La tasa de flujo del fluido a través de \(S\) es \(\displaystyle \iint_S \mathbf{v} \cdot d\mathbf{S}\). Antes de calcular esta integral de flujo, discutamos qué valor debería tener la integral. Basándonos en la Figura 10.19.4, vemos que si colocamos este cubo en el fluido (siempre y cuando el cubo no abarque el origen), entonces la tasa de fluido que entra en el cubo es la misma que la tasa de fluido que sale del cubo. El campo es rotacional en naturaleza y, para un círculo dado paralelo al plano xy que tiene un centro en el eje z, los vectores a lo largo de ese círculo son todos de la misma magnitud. Así es como podemos ver que la tasa de flujo es la misma entrando y saliendo del cubo. El flujo hacia el cubo se cancela con el flujo que sale del cubo, y por lo tanto la tasa de flujo del fluido a través del cubo debería ser cero.

Para verificar esta intuición, necesitamos calcular la integral de flujo. Calcular la integral de flujo directamente requiere dividir la integral de flujo en seis integrales de flujo separadas, una para cada cara del cubo. También necesitamos encontrar vectores tangentes, calcular su producto cruz, y usar la Ecuación 10.17.1. Sin embargo, usar el teorema de la divergencia hace que este cálculo sea mucho más rápido:

\[ \iint_S \mathbf{v} \cdot d\mathbf{S} = \iiint_C \text{div} \, (\mathbf{v}) \, dV = \iiint_C 0 \, dV = 0. \]

Por lo tanto, el flujo es cero, como se esperaba. ♦

Ejercicio de control 10.19.3

Sea \(\mathbf{v} = \left\langle \frac{x}{z}, \frac{y}{z}, 0 \right\rangle\) el campo de velocidad de un fluido. Sea \(C\) el cubo sólido dado por \(1 \leq x \leq 4\), \(2 \leq y \leq 5\), \(1 \leq z \leq 4\), y sea \(S\) la frontera de este cubo (vea la siguiente figura). Encuentre la tasa de flujo del fluido a través de \(S\).

El Ejemplo 10.19.3 ilustra una consecuencia notable del teorema de la divergencia. Sea \(S\) una superficie cerrada suave a trozos y sea \(\mathbf{F}\) un campo vectorial definido en una región abierta que contiene la superficie encerrada por \(S\). Si \(\mathbf{F}\) tiene la forma \(\mathbf{F} = \langle f(y, z), g(x, z), h(x, y) \rangle\), entonces la divergencia de \(\mathbf{F}\) es cero. Por el teorema de la divergencia, el flujo de \(\mathbf{F}\) a través de \(S\) es también cero. Esto hace que ciertas integrales de flujo sean increíblemente fáciles de calcular. Por ejemplo, suponga que queríamos calcular la integral de flujo \(\displaystyle \iint_S \mathbf{F} \cdot d\mathbf{S}\) donde \(S\) es un cubo y

\[ \mathbf{F} = \langle (\sin y) e^{yz}, x^2 z^2, \cos(xy) e^{\sin z} \rangle. \]

Calcular la integral de flujo directamente sería difícil, si no imposible, usando las técnicas que estudiamos anteriormente. Por lo menos, tendríamos que dividir la integral de flujo en seis integrales, una para cada cara del cubo. Pero, dado que la divergencia de este campo es cero, el teorema de la divergencia muestra inmediatamente que la integral de flujo es cero.

Ahora podemos usar el teorema de la divergencia para justificar la interpretación física de la divergencia que discutimos anteriormente. Recuerde que si \(\mathbf{F}\) es un campo vectorial tridimensional continuo y \(P\) es un punto en el dominio de \(\mathbf{F}\), entonces la divergencia de \(\mathbf{F}\) en \(P\) es una medida del “flujo neto hacia afuera” de \(\mathbf{F}\) en \(P\). Si \(\mathbf{F}\) representa el campo de velocidad de un fluido, entonces la divergencia de \(\mathbf{F}\) en \(P\) es una medida de la tasa de flujo neto hacia afuera desde el punto \(P\) (el flujo de fluido que sale de \(P\) menos el flujo de fluido que entra a \(P\)). Para ver cómo el teorema de la divergencia justifica esta interpretación, sea \(B_r\) una bola de radio \(r\) muy pequeño con centro en \(P\), y supongamos que \(B_r\) está en el dominio de \(\mathbf{F}\). Además, supongamos que \(B_r\) tiene una orientación positiva, hacia afuera. Dado que el radio de \(B_r\) es pequeño y \(\mathbf{F}\) es continuo, la divergencia de \(\mathbf{F}\) es aproximadamente constante en \(B_r\). Es decir, si \(P’\) es cualquier punto en \(B_r\), entonces \(\text{div} \, \mathbf{F}(P) \approx \text{div} \, \mathbf{F}(P’)\). Sea \(S_r\) denote la esfera de la frontera de \(B_r\). Podemos aproximar el flujo a través de \(S_r\) usando el teorema de la divergencia como sigue:

\[ \begin{aligned} \iint_{S_r} \mathbf{F} \cdot d\mathbf{S} &= \iiint_{B_r} \text{div} \, \mathbf{F} \, dV \\ &\approx \iiint_{B_r} \text{div} \, \mathbf{F}(P) \, dV \\ &= \text{div} \, \mathbf{F}(P) V(B_r). \end{aligned} \]

A medida que reducimos el radio \(r\) a cero a través de un límite, la cantidad \(\text{div} \, \mathbf{F}(P) V(B_r)\) se acerca arbitrariamente al flujo. Por lo tanto,

\[ \text{div} \, \mathbf{F}(P) = \lim_{r \to 0^+} \frac{1}{V(B_r)} \iint_{S_r} \mathbf{F} \cdot d\mathbf{S}, \]

y podemos considerar la divergencia en \(P\) como medir la tasa neta de flujo hacia afuera por unidad de volumen en \(P\). Dado que “flujo hacia afuera” es un término informal para la tasa neta de flujo hacia afuera por unidad de volumen, hemos justificado la interpretación física de la divergencia que discutimos anteriormente, y hemos usado el teorema de la divergencia para dar esta justificación.

Aplicación a Campos Electrostáticos

El teorema de la divergencia tiene muchas aplicaciones en física e ingeniería. Nos permite escribir muchas leyes físicas tanto en forma integral como diferencial (de la misma manera que el teorema de Stokes nos permitió traducir entre una forma integral y diferencial de la ley de Faraday). Áreas de estudio como la dinámica de fluidos, el electromagnetismo y la mecánica cuántica tienen ecuaciones que describen la conservación de la masa, el momento o la energía, y el teorema de la divergencia nos permite dar estas ecuaciones tanto en forma integral como diferencial.

Una de las aplicaciones más comunes del teorema de la divergencia es a los campos electrostáticos. Un resultado importante en este tema es la ley de Gauss. Esta ley establece que si S es una superficie cerrada en el campo electrostático E, entonces el flujo de E a través de S es la carga total encerrada por S (dividida por una constante eléctrica). Ahora usamos el teorema de la divergencia para justificar el caso especial de esta ley en el que el campo electrostático es generado por una carga puntual estacionaria en el origen.

Si \((x, y, z)\) es un punto en el espacio, entonces la distancia desde el punto al origen es \(r = \sqrt{x^2 + y^2 + z^2}\). Sea \(\mathbf{F}_r\) denote el campo vectorial radial \(\mathbf{F}_r = \frac{1}{r^2} \langle \frac{x}{r}, \frac{y}{r}, \frac{z}{r} \rangle\). El vector en una posición dada en el espacio apunta en la dirección del vector unitario radial \(\langle \frac{x}{r}, \frac{y}{r}, \frac{z}{r} \rangle\) y se escala por la cantidad \(\frac{1}{r^2}\). Por lo tanto, la magnitud de un vector en un punto dado es inversamente proporcional al cuadrado de la distancia del vector desde el origen. Suponga que tenemos una carga estacionaria de \(q\) Coulombs en el origen, que existe en el vacío. La carga genera un campo electrostático \(\mathbf{E}\) dado por

\[ \mathbf{E} = \frac{q}{4\pi \epsilon_0} \mathbf{F}_r, \]

donde la aproximación \(\epsilon_0 = 8.854 \times 10^{-12}\) farad (F)/m es una constante eléctrica. (La constante \(\epsilon_0\) es una medida de la resistencia encontrada al formar un campo eléctrico en el vacío). Note que \(\mathbf{E}\) es un campo vectorial radial similar al campo gravitacional descrito en el Ejemplo 10.12.6. La diferencia es que este campo apunta hacia afuera mientras que el campo gravitacional apunta hacia adentro. Porque

\[ \mathbf{E} = \frac{q}{4\pi \epsilon_0} \mathbf{F}_r = \frac{q}{4\pi \epsilon_0} \left( \frac{1}{r^2} \langle \frac{x}{r}, \frac{y}{r}, \frac{z}{r} \rangle \right), \]

decimos que los campos electrostáticos obedecen una ley de la inversa del cuadrado. Es decir, la fuerza electrostática en un punto dado es inversamente proporcional al cuadrado de la distancia desde la fuente de la carga (que en este caso está en el origen). Dado este campo vectorial, mostramos que el flujo a través de la superficie cerrada \(S\) es cero si la carga está afuera de \(S\), y que el flujo es \(q/\epsilon_0\) si la carga está dentro de \(S\). En otras palabras, el flujo a través de \(S\) es la carga dentro de la superficie dividida por la constante \(\epsilon_0\). Este es un caso especial de la ley de Gauss, y aquí usamos el teorema de la divergencia para justificar este caso especial.

Para mostrar que el flujo a través de \(S\) es la carga dentro de la superficie dividida por la constante \(\epsilon_0\), necesitamos dos pasos intermedios. Primero mostramos que la divergencia de \(\mathbf{F}_r\) es cero y luego mostramos que el flujo de \(\mathbf{F}_r\) a través de cualquier superficie suave \(S\) es o cero o \(4\pi\). Entonces podemos justificar este caso especial de la ley de Gauss.

Ejemplo ilustrativo 10.19.4: La Divergencia de F_r es Cero

Verificar que la divergencia de F_r es cero donde F_r está definida (lejos del origen).

Solución:

Dado que \(r = \sqrt{x^2 + y^2 + z^2}\), la regla del cociente nos da

\[ \begin{aligned} \frac{\partial}{\partial x} \left(\frac{x}{r^3}\right) &= \frac{\partial}{\partial x} \left( \frac{x}{(x^2 + y^2 + z^2)^{3/2}} \right) \\ &= \frac{(x^2 + y^2 + z^2)^{3/2} – x \left[ \frac{3}{2}(x^2 + y^2 + z^2)^{1/2} 2x \right]}{(x^2 + y^2 + z^2)^3} \\ &= \frac{r^3 – 3x^2 r}{r^6} = \frac{r^2 – 3x^2}{r^5}. \end{aligned} \]

Similarmente,

\[ \frac{\partial}{\partial y} \left(\frac{y}{r^3}\right) = \frac{r^2 – 3y^2}{r^5} \quad \text{y} \quad \frac{\partial}{\partial z} \left(\frac{z}{r^3}\right) = \frac{r^2 – 3z^2}{r^5}. \]

Por lo tanto,

\[ \begin{aligned} \text{div} \, \mathbf{F}_r &= \frac{r^2 – 3x^2}{r^5} + \frac{r^2 – 3y^2}{r^5} + \frac{r^2 – 3z^2}{r^5} \\ &= \frac{3r^2 – 3(x^2 + y^2 + z^2)}{r^5} \\ &= \frac{3r^2 – 3r^2}{r^5} = 0. \end{aligned} \]

♦

Nótese que dado que la divergencia de F_r es cero y E es F_r escalado por una constante, la divergencia del campo electrostático E también es cero (excepto en el origen).

Teorema 10.19.2: Flujo a través de una Superficie Lisa

Sea S una superficie cerrada, conexa y suave a trozos y sea \(\mathbf{F}_r = \frac{1}{r^2} \langle \frac{x}{r}, \frac{y}{r}, \frac{z}{r} \rangle\). Entonces,

\[ \iint_S \mathbf{F}_r \cdot d\mathbf{S} = \begin{cases} 0 & \text{si S no encierra el origen} \\ 4\pi & \text{si S encierra el origen}. \end{cases} \]

♦

En otras palabras, este teorema dice que el flujo de Fr a través de cualquier superficie cerrada lisa a trozos S depende solo de si el origen está dentro de S.

Prueba:

La lógica de esta prueba sigue la lógica del Ejemplo 10.15.9, solo que usamos el teorema de la divergencia en lugar del teorema de Green.

Primero, suponga que \(S\) no encierra el origen. En este caso, el sólido encerrado por \(S\) está en el dominio de \(\mathbf{F}_r\), y dado que la divergencia de \(\mathbf{F}_r\) es cero, podemos aplicar inmediatamente el teorema de la divergencia y encontrar que

\[ \iint_S \mathbf{F} \cdot d\mathbf{S} \text{ es cero.} \]

Ahora suponga que \(S\) sí encierra el origen. No podemos usar el teorema de la divergencia para calcular el flujo, porque el campo no está definido en el origen. Sea \(S_a\) una esfera de radio \(a\) dentro de \(S\) centrada en el origen. El vector normal unitario hacia afuera en la superficie de la esfera, en coordenadas esféricas, es

\[ \mathbf{t}_\phi \times \mathbf{t}_\theta = \langle a^2 \cos \theta \sin^2 \phi, a^2 \sin \theta \sin^2 \phi, a^2 \sin \phi \cos \phi \rangle \]

(ver Ejemplo 10.17.7). Por lo tanto, en la superficie de la esfera, el producto punto \(\mathbf{F}_r \cdot \mathbf{N}\) (en coordenadas esféricas) es

\[ \begin{aligned} \mathbf{F}_r \cdot \mathbf{N} &= \left\langle \frac{\sin \phi \cos \theta}{a^2}, \frac{\sin \phi \sin \theta}{a^2}, \frac{\cos \phi}{a^2} \right\rangle \cdot \langle a^2 \cos \theta \sin^2 \phi, a^2 \sin \theta \sin^2 \phi, a^2 \sin \phi \cos \phi \rangle \\ &= \sin \phi \left( \langle \sin \phi \cos \theta, \sin \phi \sin \theta, \cos \phi \rangle \cdot \langle \sin \phi \cos \theta, \sin \phi \sin \theta, \cos \phi \rangle \right) \\ &= \sin \phi. \end{aligned} \]

El flujo de \(\mathbf{F}_r\) a través de \(S_a\) es

\[ \iint_{S_a} \mathbf{F}_r \cdot \mathbf{N} \, dS = \int_0^{2\pi} \int_0^{\pi} \sin \phi \, d\phi d\theta = 4\pi. \]

Ahora, recuerde que estamos interesados en el flujo a través de \(S\), no necesariamente el flujo a través de \(S_a\). Para calcular el flujo a través de \(S\), sea \(E\) el sólido entre las superficies \(S_a\) y \(S\). Entonces, la frontera de \(E\) consta de \(S_a\) y \(S\). Denotamos esta frontera por \(S – S_a\) para indicar que \(S\) está orientada hacia afuera pero ahora \(S_a\) está orientada hacia adentro. Nos gustaría aplicar el teorema de la divergencia al sólido \(E\). Note que el teorema de la divergencia, como se indica, no puede manejar un sólido como \(E\) porque \(E\) tiene un agujero. Sin embargo, el teorema de la divergencia se puede extender para manejar regiones con agujeros, al igual que el teorema de Green se puede extender para manejar regiones con agujeros. Esto nos permite usar el teorema de la divergencia de la siguiente manera. Por el teorema de la divergencia,

\[ \iint_{S – S_a} \mathbf{F}_r \cdot d\mathbf{S} = \iint_S \mathbf{F}_r \cdot d\mathbf{S} – \iint_{S_a} \mathbf{F}_r \cdot d\mathbf{S} \] \[ = \iiint_E \text{div} \, \mathbf{F}_r \, dV = \iiint_E 0 \, dV = 0. \]

Por lo tanto,

\[ \iint_S \mathbf{F}_r \cdot d\mathbf{S} = \iint_{S_a} \mathbf{F}_r \cdot d\mathbf{S} = 4\pi, \]

y tenemos nuestro resultado deseado. ♦

Ahora regresamos a calcular el flujo a través de una superficie suave en el contexto del campo electrostático \(\mathbf{E} = \frac{q}{4\pi \epsilon_0} \mathbf{F}_r\) de una carga puntual en el origen. Sea \(\textit{S}\) una superficie cerrada suave a trozos que encierra el origen. Entonces

\[ \iint_{\textit{S}} \mathbf{E} \cdot d\mathbf{S} = \iint_{\textit{S}} \frac{q}{4\pi \epsilon_0} \mathbf{F}_r \cdot d\mathbf{S} \] \[ = \frac{q}{4\pi \epsilon_0} \iint_{\textit{S}} \mathbf{F}_r \cdot d\mathbf{S} \] \[ = \frac{q}{\epsilon_0}. \]

Si \(\textit{S}\) no encierra el origen, entonces

\[ \iint_{\textit{S}} \mathbf{E} \cdot d\mathbf{S} = \frac{q}{4\pi \epsilon_0} \iint_{\textit{S}} \mathbf{F}_r \cdot d\mathbf{S} = 0. \]

Por lo tanto, hemos justificado la afirmación que nos propusimos justificar: el flujo a través de la superficie cerrada \(\textit{S}\) es cero si la carga está fuera de \(\textit{S}\), y el flujo es \(q/\epsilon_0\) si la carga está dentro de \(\textit{S}\).

Este análisis solo funciona si hay una sola carga puntual en el origen. En este caso, la ley de Gauss dice que el flujo de \(\mathbf{E}\) a través de \(\textit{S}\) es la carga total encerrada por \(\textit{S}\). La ley de Gauss se puede extender para manejar múltiples sólidos cargados en el espacio, no solo una sola carga puntual en el origen. La lógica es similar al análisis anterior, pero más allá del alcance de este texto. En total generalidad, la ley de Gauss establece que si \(\textit{S}\) es una superficie cerrada suave a trozos y \(Q\) es la cantidad total de carga dentro de \(\textit{S}\), entonces el flujo de \(\mathbf{E}\) a través de \(\textit{S}\) es \(Q/\epsilon_0\).

Ejemplo ilustrativo 10.19.5: Usando la ley de Gauss

Supongamos que tenemos cuatro cargas puntuales estacionarias en el espacio, todas con una carga de 0.002 Coulombs (C). Las cargas están ubicadas en \((0, 1, 1)\), \((1, 1, 4)\), \((-1, 0, 0)\), y \((-2, -2, 2)\). Sea \(\mathbf{E}\) denota el campo electrostático generado por estas cargas puntuales. Si \(S\) es la esfera de radio 2 orientada hacia afuera y centrada en el origen, entonces encuentre

\[ \iint_S \mathbf{E} \cdot d\mathbf{S}. \]

Saludos:

De acuerdo con la ley de Gauss, el flujo de \(\mathbf{E}\) a través de \(\textit{S}\) es la carga total dentro de \(\textit{S}\) dividida por la constante eléctrica. Dado que \(\textit{S}\) tiene radio 2, note que solo dos de las cargas están dentro de \(\textit{S}\): la carga en \((0, 1, 1)\) y la carga en \((-1, 0, 0)\). Por lo tanto, la carga total encerrada por \(\textit{S}\) es 0.004 y, por la ley de Gauss,

\[ \iint_{\textit{S}} \mathbf{E} \cdot d\mathbf{S} = \frac{0.004}{8.854 \times 10^{-12}} \approx 4.518 \times 10^9 \, \text{V} \cdot \text{m}. \]

♦

Ejercicio de control 10.19.4

Resuelva el ejemplo anterior para la superficie S que es una esfera de radio 4 centrada en el origen, orientada hacia afuera. ♦