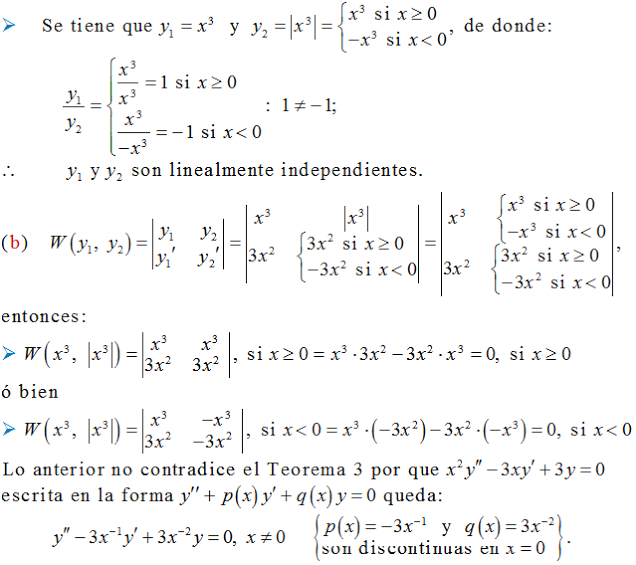Capítulo 3.1
(Índice del libro ED de Edwards y Penney)
En los problemas del 1 al 16 se proporciona una ecuación diferencial lineal de segundo orden homogénea, dos funciones y1 y y2 y un par de condiciones iniciales. Verifique primero que y1 y y2 son soluciones de la ecuación diferencial. Posteriormente, encuentre una solución particular de la forma y = c1 y1 + c2 y2 que satisfaga las condiciones iniciales dadas. Las primas significan derivadas con respecto a x.
1. 
(Vea la solución del Ejercicio 3.1_1)
2. 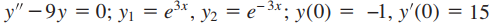
(Vea la solución del Ejercicio 3.1_2)
3. 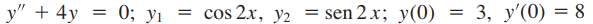
(Vea la solución del Ejercicio 3.1_3)
4. 
(Vea la solución del Ejercicio 3.1_4)
5. 
(Vea la solución del Ejercicio 3.1_5)
6. 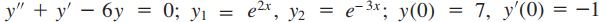
(Vea la solución del Ejercicio 3.1_6)
7. 
(Vea la solución del Ejercicio 3.1_7)
8. 
(Vea la solución del Ejercicio 3.1_8)
9. 
(Vea la solución del Ejercicio 3.1_9)
10. 
(Vea la solución del Ejercicio 3.1_10)
11. 
(Vea la solución del Ejercicio 3.1_11)
12. 
(Vea la solución del Ejercicio 3.1_12)
13. 
(Vea la solución del Ejercicio 3.1_13)
14. 
(Vea la solución del Ejercicio 3.1_14)
15. 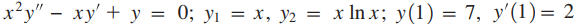
(Vea la solución del Ejercicio 3.1_15)
16. 
(Vea la solución del Ejercicio 3.1_16)
En los tres problemas siguientes ilustre el hecho de que el principio de superposición generalmente no se cumple para ecuaciones no lineales.


(Vea la solución del Ejercicio 3.1_17)

(Vea la solución del Ejercicio 3.1_18)

(Vea la solución del Ejercicio 3.1_19)
Determine cuál de los pares de funciones en los problemas 20 al 26 son linealmente independientes o dependientes en toda la recta real.

(Vea la solución del Ejercicio 3.1_20)

(Vea la solución del Ejercicio 3.1_21)

(Vea la solución del Ejercicio 3.1_22)

(Vea la solución del Ejercicio 3.1_23)

(Vea la solución del Ejercicio 3.1_24)
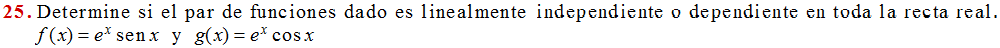
(Vea la solución del Ejercicio 3.1_25)

(Vea la solución del Ejercicio 3.1_26)

(Vea la solución del Ejercicio 3.1_27)

(Vea la solución del Ejercicio 3.1_28)

(Vea la solución del Ejercicio 3.1_29)

(Vea la solución del Ejercicio 3.1_30)

(Vea la solución del Ejercicio 3.1_31)
Aplique los teoremas 5 y 6 para encontrar las soluciones generales de las ecuaciones diferenciales dadas en los problemas 33 al 42. Las primas significan derivadas con respecto a x.
33. 
(Vea la solución del Ejercicio 3.1_33)
34. 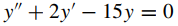
(Vea la solución del Ejercicio 3.1_34)
35. 
(Vea la solución del Ejercicio 3.1_35)
36. 
(Vea la solución del Ejercicio 3.1_36)
37. 
(Vea la solución del Ejercicio 3.1_37)
38. 
(Vea la solución del Ejercicio 3.1_38)
39. 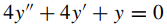
(Vea la solución del Ejercicio 3.1_39)
40. 
(Vea la solución del Ejercicio 3.1_40)
41. 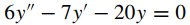
(Vea la solución del Ejercicio 3.1_41)
42. 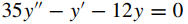
(Vea la solución del Ejercicio 3.1_42)

(Vea la solución del Ejercicio 3.1_43)

(Vea la solución del Ejercicio 3.1_44)

(Vea la solución del Ejercicio 3.1_45)

(Vea la solución del Ejercicio 3.1_46)

(Vea la solución del Ejercicio 3.1_47)

(Vea la solución del Ejercicio 3.1_48)
49. Encuentre el punto más alto de la curva solución con y(0) = 1 y y′(0) = 6 en la figura 3.1.6.
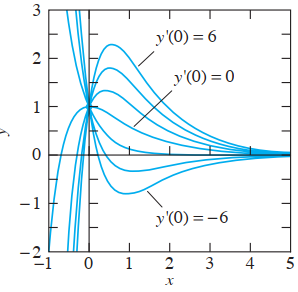
( FIGURA 3.1.6. Soluciones de y″ + 3y′ + 2y = 0 con el mismo valor inicial y(0) = 1, pero con
pendientes iniciales diferentes.)
(Vea la solución del Ejercicio 3.1_49)
51. La ecuación de Euler de segundo orden es de la forma

(Vea la solución del Ejercicio 3.1_51)
Lleve a cabo la sustitución v = ln x del problema 51 para encontrar las soluciones generales (para x > 0) de las ecuaciones de Euler en los problemas 52 al 56.
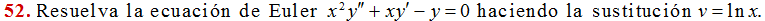
(Vea la solución del Ejercicio 3.1_52)

(Vea la solución del Ejercicio 3.1_53)

(Vea la solución del Ejercicio 3.1_54)
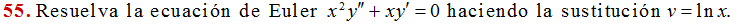
(Vea la solución del Ejercicio 3.1_55)

(Vea la solución del Ejercicio 3.1_56)
Soluciones 3.1 (en imagen)