| 12. Integración múltiple | 12.1 Integrales dobles sobre regiones rectangulares |

Ejercicios propuestos para el Capítulo 12.1

En los siguientes ejercicios, use la regla del punto medio con $m = 4$ y $n = 2$ para estimar el volumen del sólido delimitado por la superficie $z = f(x, y)$, los planos verticales $x = 1$, $x = 2$, $y = 1$ y $y = 2$, y el plano horizontal $z = 0$.

  1. $f(x, y) = 4x + 2y + 8xy$
  2. $f(x, y) = 16x^2 + \dfrac{y}{2}$

En los siguientes ejercicios, estime $\iint_R f(x, y) \, dA$ usando una suma de Riemann con $m = n = 2$ y los puntos de muestra como las esquinas inferiores izquierdas de los subrectángulos de la partición.

  1. $f(x, y) = \sin x – \cos y, \quad R = [0, \pi] \times [0, \pi]$
  2. $f(x, y) = \cos x + \cos y, \quad R = [0, \pi] \times [0, \frac{\pi}{2}]$

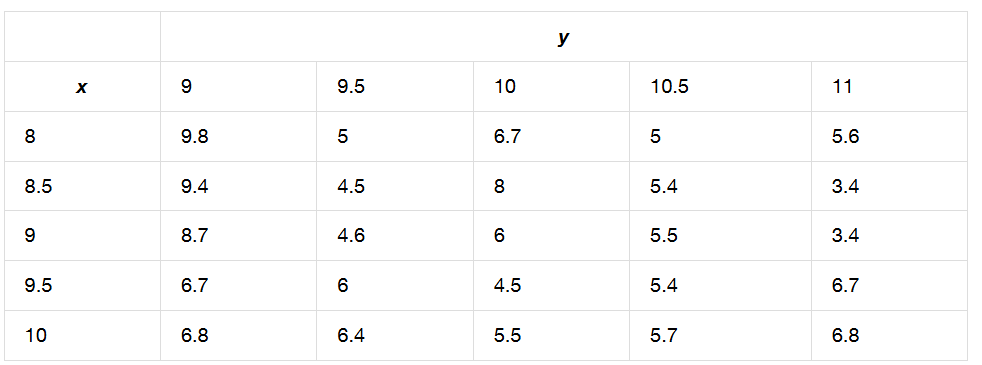
5. Use la regla del punto medio con $m = n = 2$ para estimar $\iint_R f(x, y) \, dA$, donde los valores de la función $f$ en $R = [8, 10] \times [9, 11]$ se dan en la siguiente tabla.

6. Los valores de la función $f$ en el rectángulo $R = [0, 2] \times [7, 9]$ se dan en la siguiente tabla. Estime la integral doble $\iint_R f(x, y) \, dA$ usando una suma de Riemann con $m = n = 2$. Seleccione los puntos de muestra como las esquinas superiores derechas de los subcuadrados de $R$.

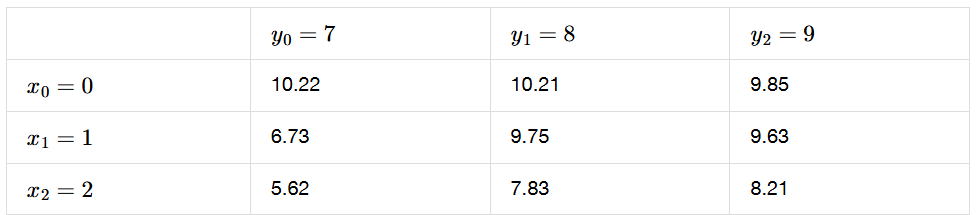
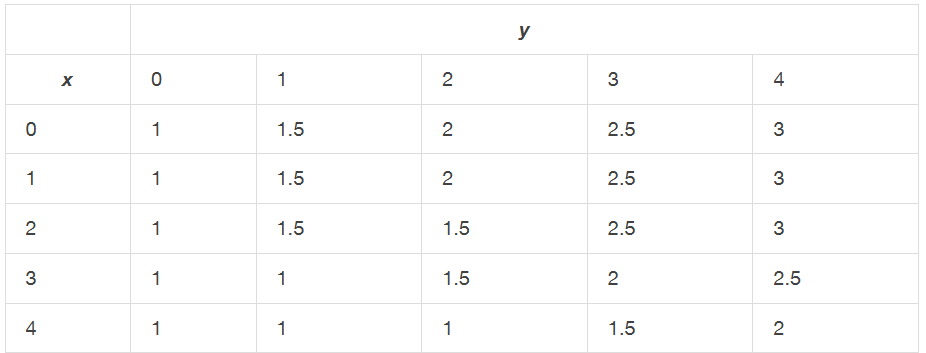
7. La profundidad de una piscina para niños de 4 pies por 4 pies, medida en intervalos de 1 pie, se da en la siguiente tabla.

  • a. Estime el volumen de agua en la piscina usando una suma de Riemann con $m = n = 2$. Seleccione los puntos de muestra usando la regla del punto medio en $R = [0, 4] \times [0, 4]$.
  • b. Aproxime la profundidad promedio de la piscina.

8. La profundidad de un agujero en el suelo de 3 pies por 3 pies, medida en intervalos de 1 pie, se da en la siguiente tabla.

  • a. Estime el volumen del agujero usando una suma de Riemann con $m = n = 3$ y los puntos de muestra como las esquinas superiores izquierdas de los subcuadrados de $R$.
  • b. Aproxime la profundidad promedio del agujero.

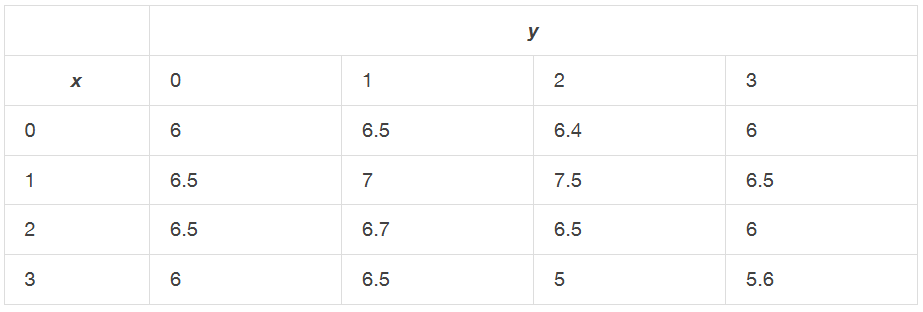
9. Las curvas de nivel $f(x, y) = k$ de la función $f$ se dan en la siguiente gráfica, donde $k$ es una constante.

  • a. Aplique la regla del punto medio con $m = n = 2$ para estimar la integral doble $\iint_R f(x, y) \, dA$, donde $R = [0.2, 1] \times [0, 0.8]$.
  • b. Estime el valor promedio de la función $f$ en $R$.

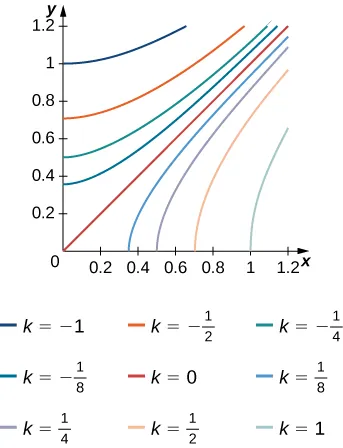
10. Las curvas de nivel $f(x, y) = k$ de la función $f$ se dan en la siguiente gráfica, donde $k$ es una constante.

  • a. Aplique la regla del punto medio con $m = n = 2$ para estimar la integral doble $\iint_R f(x, y) \, dA$, donde $R = [0.1, 0.5] \times [0.1, 0.5]$.
  • b. Estime el valor promedio de la función $f$ en $R$.

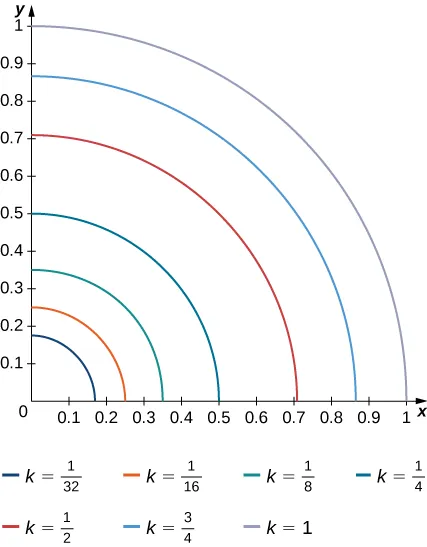
11. El sólido que se encuentra debajo de la superficie $z = \sqrt{4 – y^2}$ y por encima de la región rectangular $R = [0, 2] \times [0, 2]$ se ilustra en la siguiente gráfica. Evalúe la integral doble $\iint_R f(x, y) \, dA$, donde $f(x, y) = \sqrt{4 – y^2}$, encontrando el volumen del sólido correspondiente.

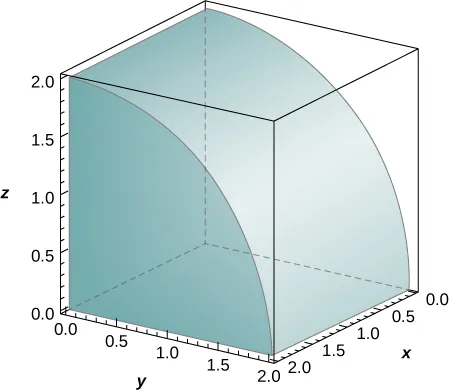
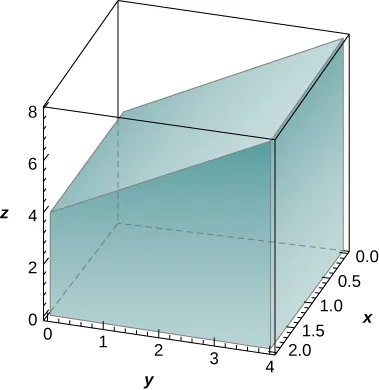
12. El sólido que se encuentra debajo del plano $z = y + 4$ y por encima de la región rectangular $R = [0, 2] \times [0, 4]$ se ilustra en la siguiente gráfica. Evalúe la integral doble $\iint_R f(x, y) \, dA$, donde $f(x, y) = y + 4$, encontrando el volumen del sólido correspondiente.

En los siguientes ejercicios, calcule las integrales intercambiando el orden de integración.

  1. $\int_{-1}^{1} \left( \int_{-2}^{2} (2x + 3y + 5) \, dx \right) \, dy$
  2. $\int_{0}^{2} \left( \int_{0}^{1} (x + 2e^y – 3) \, dx \right) \, dy$
  3. $\int_{1}^{27} \left( \int_{1}^{2} (\sqrt[3]{x} + \sqrt[3]{y}) \, dy \right) \, dx$
  4. $\int_{1}^{16} \left( \int_{1}^{8} (\sqrt[4]{x} + 2\sqrt[3]{y}) \, dy \right) \, dx$
  5. $\int_{\ln 2}^{\ln 3} \left( \int_{0}^{1} e^{x+y} \, dy \right) \, dx$
  6. $\int_{0}^{2} \left( \int_{0}^{1} 3^{x+y} \, dy \right) \, dx$
  7. $\int_{1}^{6} \left( \int_{2}^{9} \dfrac{\sqrt{y}}{x^2} \, dy \right) \, dx$
  8. $\int_{1}^{9} \left( \int_{4}^{2} \dfrac{\sqrt{x}}{y^2} \, dy \right) \, dx$

En los siguientes ejercicios, evalúe las integrales iteradas eligiendo el orden de integración.

  1. $\int_{0}^{\pi} \int_{0}^{\pi/2} \sin(2x)\cos(3y) \, dx \, dy$
  2. $\int_{\pi/12}^{\pi/8} \int_{\pi/4}^{\pi/3} [\cot x + \tan(2y)] \, dx \, dy$
  3. $\int_{1}^{e} \int_{1}^{e} \left[ \dfrac{1}{x} \sin(\ln x) + \dfrac{1}{y} \cos(\ln y) \right] \, dx \, dy$
  4. $\int_{1}^{e} \int_{1}^{e} \dfrac{\sin(\ln x)\cos(\ln y)}{xy} \, dx \, dy$
  5. $\int_{1}^{2} \int_{1}^{2} \left( \dfrac{\ln y}{x} + \dfrac{x}{2y + 1} \right) \, dy \, dx$
  6. $\int_{1}^{e} \int_{1}^{2} x^2 \ln(x) \, dy \, dx$
  7. $\int_{1}^{\sqrt{3}} \int_{1}^{2} y \arctan\left(\dfrac{1}{x}\right) \, dy \, dx$
  8. $\int_{0}^{1} \int_{0}^{1/2} (\arcsin x + \arcsin y) \, dy \, dx$
  9. $\int_{0}^{1} \int_{1}^{2} xe^{x + 4y} \, dy \, dx$
  10. $\int_{1}^{2} \int_{0}^{1} xe^{x – y} \, dy \, dx$
  11. $\int_{1}^{e} \int_{1}^{e} \left( \dfrac{\ln y}{\sqrt{y}} + \dfrac{\ln x}{\sqrt{x}} \right) \, dy \, dx$
  12. $\int_{1}^{e} \int_{1}^{e} \left( \dfrac{x \ln y}{\sqrt{y}} + \dfrac{y \ln x}{\sqrt{x}} \right) \, dy \, dx$
  13. $\int_{0}^{1} \int_{1}^{2} \left( \dfrac{x}{x^2 + y^2} \right) \, dy \, dx$
  14. $\int_{0}^{1} \int_{1}^{2} \dfrac{y}{x + y^2} \, dy \, dx$

En los siguientes ejercicios, encuentre el valor promedio de la función sobre los rectángulos dados.

  1. $f(x, y) = -x + 2y, R = [0, 1] \times [0, 1]$
  2. $f(x, y) = x^4 + 2y^3, R = [1, 2] \times [2, 3]$
  3. $f(x, y) = \sinh x + \sinh y, R = [0, 1] \times [0, 2]$
  4. $f(x, y) = \arctan(xy), R = [0, 1] \times [0, 1]$

39. Sean $f$ y $g$ dos funciones continuas tales que $0 \leq m_1 \leq f(x) \leq M_1$ para cualquier $x \in [a, b]$ y $0 \leq m_2 \leq g(y) \leq M_2$ para cualquier $y \in [c, d]$. Demuestre que la siguiente desigualdad es verdadera:

$$m_1 m_2 (b – a)(d – c) \leq \int_a^b \int_c^d f(x)g(y) \, dy \, dx \leq M_1 M_2 (b – a)(d – c)$$

En los siguientes ejercicios, use la propiedad v. de las integrales dobles y la respuesta del ejercicio anterior para demostrar que las siguientes desigualdades son verdaderas.

  1. $\dfrac{1}{e^2} \leq \iint_R e^{-x^2-y^2} \, dA \leq 1$, donde $R = [0, 1] \times [0, 1]$
  2. $\dfrac{\pi^2}{144} \leq \iint_R \sin x \cos y \, dA \leq \dfrac{\pi^2}{48}$, donde $R = [\frac{\pi}{6}, \frac{\pi}{3}] \times [\frac{\pi}{6}, \frac{\pi}{3}]$
  3. $0 \leq \iint_R e^{-y} \cos x \, dA \leq \left( \dfrac{\pi}{2} \right)^2$, donde $R = [0, \frac{\pi}{2}] \times [0, \frac{\pi}{2}]$
  4. $0 \leq \iint_R (\ln x)(\ln y) \, dA \leq (e – 1)^2$, donde $R = [1, e] \times [1, e]$

44. Sean $f$ y $g$ dos funciones continuas tales que $0 \leq m_1 \leq f(x) \leq M_1$ para cualquier $x \in [a, b]$ y $0 \leq m_2 \leq g(y) \leq M_2$ para cualquier $y \in [c, d]$. Demuestre que la siguiente desigualdad es verdadera:

$$(m_1 + m_2)(b – a)(d – c) \leq \int_a^b \int_c^d [f(x) + g(y)] \, dy \, dx \leq (M_1 + M_2)(b – a)(d – c)$$

En los siguientes ejercicios, use la propiedad v. de las integrales dobles y la respuesta del ejercicio anterior para demostrar que las siguientes desigualdades son verdaderas.

  1. $\dfrac{2}{e} \leq \iint_R (e^{-x^2} + e^{-y^2}) \, dA \leq 2$, donde $R = [0, 1] \times [0, 1]$
  2. $\dfrac{\pi^2}{36} \leq \iint_R (\sin x + \cos y) \, dA \leq \dfrac{\pi^2 \sqrt{3}}{36}$, donde $R = \left[\frac{\pi}{6}, \frac{\pi}{3}\right] \times \left[\frac{\pi}{6}, \frac{\pi}{3}\right]$
  3. $\dfrac{\pi^2}{4} e^{-\frac{\pi}{2}} \leq \iint_R (\cos x + e^{-y}) \, dA \leq \dfrac{\pi^2}{2}$, donde $R = \left[0, \frac{\pi}{2}\right] \times \left[0, \frac{\pi}{2}\right]$
  4. $0 \leq \iint_R (\ln x + \ln y) \, dA \leq 2(e – 1)^2$, donde $R = [1, e] \times [1, e]$

En los siguientes ejercicios, la función $f$ se da en términos de integrales dobles.

  • Determine la forma explícita de la función $f$.
  • Encuentre el volumen del sólido bajo la superficie $z = f(x, y)$ y por encima de la región $R$.
  • Encuentre el valor promedio de la función $f$ en $R$.
  • Use un sistema de álgebra computacional (CAS) para graficar $z = f(x, y)$ y $z = f_{\text{prom}}$ en el mismo sistema de coordenadas.
  1. [T] $f(x, y) = \int_0^y \int_0^x (xs + yt) \, ds \, dt$, donde $(x, y) \in R = [0, 1] \times [0, 1]$
  2. [T] $f(x, y) = \int_0^x \int_0^y [\cos(s) + \cos(t)] \, dt \, ds$, donde $(x, y) \in R = [0, 3] \times [0, 3]$

51. Demuestre que si $f$ y $g$ son continuas en $[a, b]$ y $[c, d]$, respectivamente, entonces:

$$\int_a^b \int_c^d [f(x) + g(y)] \, dy \, dx = (d – c) \int_a^b f(x) \, dx + \int_a^b \int_c^d g(y) \, dy \, dx$$ $$= (b – a) \int_c^d g(y) \, dy + \int_c^d \int_a^b f(x) \, dx \, dy.$$

52. Demuestre que:

$$\int_a^b \int_c^d [yf(x) + xg(y)] \, dy \, dx = \frac{1}{2}(d^2 – c^2) \left( \int_a^b f(x) \, dx \right) + \frac{1}{2}(b^2 – a^2) \left( \int_c^d g(y) \, dy \right).$$

53. [T] Considere la función $f(x, y) = e^{-x^2-y^2}$, donde $(x, y) \in R = [-1, 1] \times [-1, 1]$.

  • Use la regla del punto medio con $m = n = 2, 4, \dots, 10$ para estimar la integral doble $I = \iint_R e^{-x^2-y^2} \, dA$. Redondee sus respuestas a las centésimas más cercanas.
  • Para $m = n = 2$, encuentre el valor promedio de $f$ sobre la región $R$. Redondee su respuesta a la centésima más cercana.
  • Use un CAS para graficar en el mismo sistema de coordenadas el sólido cuyo volumen está dado por $\iint_R e^{-x^2-y^2} \, dA$ y el plano $z = f_{\text{prom}}$.

54. [T] Considere la función $f(x, y) = \sin(x^2) \cos(y^2)$, donde $(x, y) \in R = [-1, 1] \times [-1, 1]$.

  • Use la regla del punto medio con $m = n = 2, 4, \dots, 10$ para estimar la integral doble $I = \iint_R \sin(x^2) \cos(y^2) \, dA$. Redondee sus respuestas a las centésimas más cercanas.
  • Para $m = n = 2$, encuentre el valor promedio de $f$ sobre la región $R$. Redondee su respuesta a la centésima más cercana.
  • Use un CAS para graficar en el mismo sistema de coordenadas el sólido cuyo volumen está dado por $\iint_R \sin(x^2) \cos(y^2) \, dA$ y el plano $z = f_{\text{prom}}$.

En los siguientes ejercicios, se dan las funciones $f_n$, donde $n \geq 1$ es un número natural.

  • Encuentre el volumen de los sólidos $S_n$ bajo las superficies $z = f_n(x, y)$ y por encima de la región $R$.
  • Determine el límite de los volúmenes de los sólidos $S_n$ a medida que $n$ aumenta sin límite.

55. $f_n(x, y) = x^n + y^n + xy, (x, y) \in R = [0, 1] \times [0, 1]$

56. $f_n(x, y) = \dfrac{1}{x^n} + \dfrac{1}{y^n}, (x, y) \in R = [1, 2] \times [1, 2]$

57. Demuestre que el valor promedio de una función $f$ en una región rectangular $R = [a, b] \times [c, d]$ es:

$$f_{\text{prom}} \approx \frac{1}{mn} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*, y_{ij}^*)$$

donde $(x_{ij}^*, y_{ij}^*)$ son los puntos de muestra de la partición de $R$, con $1 \leq i \leq m$ y $1 \leq j \leq n$.

58. Use la regla del punto medio con $m = n$ para demostrar que el valor promedio de una función $f$ en una región rectangular $R = [a, b] \times [c, d]$ se aproxima por:

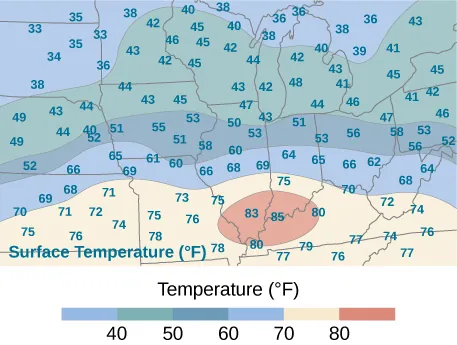
$$f_{\text{prom}} \approx \frac{1}{n^2} \sum_{i,j=1}^n f\left( \frac{1}{2}(x_{i-1} + x_i), \frac{1}{2}(y_{j-1} + y_j) \right)$$

59. Un mapa de isotermas es un gráfico que conecta puntos que tienen la misma temperatura en un momento dado durante un período de tiempo determinado. Use el ejercicio anterior y aplique la regla del punto medio con \( m=n=2 \) para hallar la temperatura promedio sobre la región dada en la siguiente figura.

Páginas: 1 2